题目内容
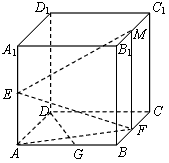
已知点E、F、G分别是正方体ABCD-A1B1C1D1的棱AA1、BC、AB的中点,
(1)求直线EF和平面ABCD所成角的正切值;
(2)求证:DG⊥EF;
(3)在棱B1C1上求一点M,使得DG⊥平面EFM。
(1)求直线EF和平面ABCD所成角的正切值;
(2)求证:DG⊥EF;
(3)在棱B1C1上求一点M,使得DG⊥平面EFM。
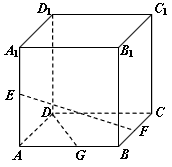
| (1)解:在正方体AC1中, ∵AA1⊥AD,AA1⊥AB, ∴AA1⊥平面ABCD,连结AF, 则∠EFA就是EF与平面ABCD所成的角, 设正方体棱长为a, ∵点F是BC的中点, ∴AF= 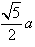 , ,而AE= 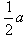 , ,则在Rt△EAF中,tan∠EAF= 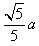 为所求。 为所求。(2)证明:在正方形ABCD中, ∵G是AB的中点,F是BC的中点, ∴DG⊥AF, ∵EA⊥平面ABCD,由三垂线定理, ∴DG⊥EF; (3)解:当点M在棱B1C1的中点时,DG⊥平面EFM; 证明如下:连结MF、EM, ∵F是BC的中点, ∴MF∥BB1, ∵BB1∥AA1, ∴MF∥AA1, ∵AA1⊥平面ABCD, ∴MF⊥平面ABCD, ∴MF⊥DG, ∵DG⊥EF, ∴DG⊥平面EFM。 |
 |

练习册系列答案
相关题目
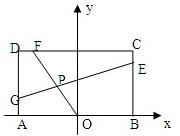 已知常数a>0,在矩形ABCD中,AB=4,BC=4a,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且
已知常数a>0,在矩形ABCD中,AB=4,BC=4a,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且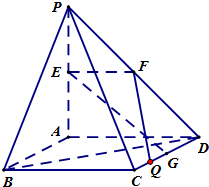 (理)如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,点E、F、G分别为线段PA、PD和CD的中点.
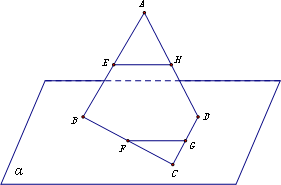
(理)如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,点E、F、G分别为线段PA、PD和CD的中点.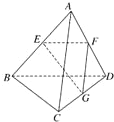 如图所示,已知空间四边形的每条边和对角线长都等于a,点E、F、G分别为AB、AD、DC的中点,则a2等于( )
如图所示,已知空间四边形的每条边和对角线长都等于a,点E、F、G分别为AB、AD、DC的中点,则a2等于( ) 如图,已知常数a>0,在矩形ABCD中,AB=4,BC=4a,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且
如图,已知常数a>0,在矩形ABCD中,AB=4,BC=4a,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且