题目内容
若点P是棱长为1的正方体ABCD-A1B1C1D1中异于A的一个顶点，则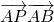
的所有可能值的个数是
- A.1
- B.2
- C.3
- D.4
B
分析：根据立方体的八个顶点分成两类：一类是：当P点是A1，D，D1中的一个时；另一类是：当P点是B，C，C1，B1中的一个时，分别根据向量数量积的几何意义得：
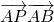=1，从而得出的所有可能值的个数．
解答：
解：分成两类：
一类是：当P点是A1，D，D1中的一个时，此时
，
∴
；
另一类是：当P点是B，C，C1，B1中的一个时，此时
方向上的投影是AB，
根据向量数量积的几何意义得：=1；
则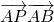的所有可能值的个数是0或1．
故选B．
点评：此题主要考查了向量在几何中的应用以及立体图形的性质，得出立方体的八个顶点分成二类是解决问题的关键．
分析：根据立方体的八个顶点分成两类：一类是：当P点是A1，D，D1中的一个时；另一类是：当P点是B，C，C1，B1中的一个时，分别根据向量数量积的几何意义得：
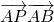=1，从而得出的所有可能值的个数．解答：
解：分成两类：一类是：当P点是A1，D，D1中的一个时，此时
，∴
；另一类是：当P点是B，C，C1，B1中的一个时，此时
方向上的投影是AB，根据向量数量积的几何意义得：
=1；则
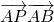的所有可能值的个数是0或1．故选B．
点评：此题主要考查了向量在几何中的应用以及立体图形的性质，得出立方体的八个顶点分成二类是解决问题的关键．
练习册系列答案
相关题目
如图，P-ABC是底面边长为1的正三棱锥，D、E、F分别为棱长PA、PB、PC上的点，截面DEF∥底面ABC，且棱台DEF-ABC与棱锥P-ABC的棱长和相等．（棱长和是指多面体中所有棱的长度之和）
（2009•闵行区二模）（文）如图几何体是由一个棱长为2的正方体ABCD-A1B1C1D1与一个侧棱长为2的正四棱锥P-A1B1C1D1组合而成．