Question

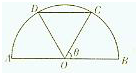农户计划将已有的一块半径为100米的土地（如图所示）重新规划，拟将面积相等的两个△AOD与△BOC置为普通花草地，△COD置为特级花草地，O为半圆圆心，∠COB=θ，据市场调查，特级花草市场销售价变化不大，普通花草市场销售价变化较大，以往经验显示：特级花草地每平方米年利润为a元，普通花草地每平方米年利润为asinθ元．
（1）分别写出△BOC、△AOD、△COD的面积关于θ的函数关系；
（2）写出农户年总利润f（θ）关于θ的函数关系，当θ为何值时，年总利润f（θ）最大．

Answer 1

分析：（1）根据三角形的面积等于

1

2

absinC，求出S_△BOC、S_△AOD 以及S_△COD的值．
（2）农户年总利润f（θ）等于特级花草地的利润加上普通花草地的利润，再利用三角恒等变换化简f（θ）为50

2

asin（2θ-

π

4

）+50a，再利用正弦函数的性质求出f（θ）的最大值以及f（θ）最大时θ的值．

解答：解：（1）由题意可得 S_△BOC=

1

2

×102 sinθ=S_△AOD，其中 0＜θ＜

π

2

．
S_△COD=

1

2

×102sin（π-2θ）=

1

2

×102sin2θ．
（2）农户年总利润f（θ）等于特级花草地的利润加上普通花草地的利润，而年利润等于每平方米年利润乘以面积，
故f（θ）=a•

1

2

×102sin2θ+asinθ•（2•

1

2

×102 sinθ ）
=50asin2θ+100a•sin²θ=50asin2θ+100a

1-cos2θ

2

=50asin2θ-50acos2θ+50a
=50

2

a sin（2θ-

π

4

）+50a．
故当2θ-

π

4

=

π

2

，即θ=

3π

8

时，总利润f（θ）取得最大值．

点评：本题主要考查三角函数的模型的应用，正弦函数的值域以及正弦函数取得最大值的条件，属于中档题．