题目内容
5.某共享单车公司欲在某社区投放一批共享单车,单车总数不超过100辆,现有A,B两种型号的单车:其中A型为运动型,成本为500元/车,骑行半小时需花费0.5元;B型车为轻便型,成本为3000元/车,骑行半小时需花费1元.若公司投入成本资金不能超过10万元,且投入的车辆平均每车每天会被骑行2次,每次不超过半小时(不足半小时按半小时计算),则在该社区单车公司可获得的总收入最多为120元.分析 根据题意,设投放A型号单车x辆,B型号单车y辆,单车公司可获得的总收入为Z;分析可得$\left\{\begin{array}{l}{x+y≤100}\\{500x+3000y≤100000}\\{x≥0,x∈Z}\\{y≥0,y∈Z}\end{array}\right.$,且Z=2×0.5x+2×y=x+2y,化简不等式组表示的平面区域,分析可得Z的最大值,即可得答案.
解答 解:根据题意,设投放A型号单车x辆,B型号单车y辆,单车公司可获得的总收入为Z;
则有$\left\{\begin{array}{l}{x+y≤100}\\{500x+3000y≤100000}\\{x≥0,x∈Z}\\{y≥0,y∈Z}\end{array}\right.$,即$\left\{\begin{array}{l}{x+y≤100}\\{x+6y≤200}\\{x≥0,x∈Z}\\{y≥0,y∈Z}\end{array}\right.$,①
且Z=2×0.5x+2×y=x+2y,
不等式组①表示的平面区域为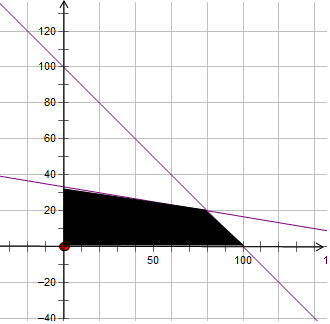 ;
;
分析可得:当x=80,y=20时,
Z取得最大值,其最大值Z=80+2×20=120;
故答案为:120.
点评 本题考查线性规划问题的应用,注意本题中x、y的取值范围.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
15.若直线l1:mx-3y-2=0与直线l2:(2-m)x-3y+5=0互相平行,则实数m的值为( )
| A. | 2 | B. | -1 | C. | 1 | D. | 0 |
13.若G为△ABC的重心,则( )
| A. | $\overrightarrow{AG}$=$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AC}$ | B. | $\overrightarrow{AG}$=$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$ | C. | $\overrightarrow{AG}$=$\frac{1}{2}$$\overrightarrow{AB}$-$\frac{1}{2}$$\overrightarrow{AC}$ | D. | $\overrightarrow{AG}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$ |
20.cos3tan4的值( )
| A. | 小于0 | B. | 大于0 | C. | 等于0 | D. | 不存在 |