题目内容
若关于x的方程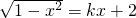 恰有两个实根,则k的取值范围是________.
恰有两个实根,则k的取值范围是________.
 ∪
∪
分析:令y=
 表示以(0,0)为圆心以1为半径的上半圆,直线y1=kx+2过(0,2),关于x的方程
表示以(0,0)为圆心以1为半径的上半圆,直线y1=kx+2过(0,2),关于x的方程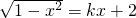 恰有两个实根,则直线y=kx+2与半圆有2个交点,结合图形可求
恰有两个实根,则直线y=kx+2与半圆有2个交点,结合图形可求解答:令y=
 表示以(0,0)为圆心以1为半径的上半圆,直线y1=kx+2过(0,2)
表示以(0,0)为圆心以1为半径的上半圆,直线y1=kx+2过(0,2)关于x的方程
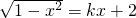 恰有两个实根,则直线y=kx+2与半圆有2个交点
恰有两个实根,则直线y=kx+2与半圆有2个交点∵
 可得
可得 即此时直线与圆相切时,k=
即此时直线与圆相切时,k=
当直线过(-1,0)时,斜率K=2,过(1,0))时斜率K=-2
结合图形可知,满足条件

故答案为:


点评:本题主要考查了直线与圆的位置关系的应用,解题的关键是要能发现出函数对应的图形,体现了数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
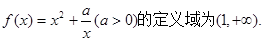
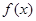 在其定义域上的单调性;
在其定义域上的单调性;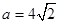 时,若关于x的方程
时,若关于x的方程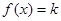 恰有两个不等实根,求实数k的取值范围。
恰有两个不等实根,求实数k的取值范围。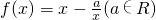 ,g(x)=lnx.
,g(x)=lnx.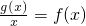 恰有两个不等的实根,求a的取值范围.
恰有两个不等的实根,求a的取值范围.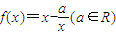 ,g(x)=lnx.
,g(x)=lnx.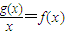 恰有两个不等的实根,求a的取值范围.
恰有两个不等的实根,求a的取值范围. ,g(x)=lnx.
,g(x)=lnx.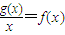 恰有两个不等的实根,求a的取值范围.
恰有两个不等的实根,求a的取值范围.