题目内容
已知函数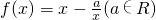 ,g(x)=lnx.
,g(x)=lnx.
(Ⅰ)求函数F(x)=f(x)+g(x)的单调区间;
(Ⅱ)若关于x的方程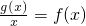 恰有两个不等的实根,求a的取值范围.
恰有两个不等的实根,求a的取值范围.
解:(Ⅰ)函数F(x)的定义域为(0,+∞)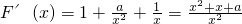 …(1分)
…(1分)
①当a≥0时,F'(x)>0,F(x)的单调增区间为(0,+∞),无单调减区间 …(3分)
②当a<0时,方程x2+x+a=0的两根为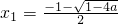 ,
,
当 时,F'(x)<0
时,F'(x)<0
当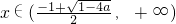 时,F'(x)>0
时,F'(x)>0
综上所述,a≥0时,F(x)的单调增区间为(0,+∞),无单调减区间a<0时,F(x)的单调增区间为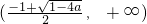 ,单调减区间为
,单调减区间为 …(6分)
…(6分)
(Ⅱ) …(7分)
…(7分)
令G(x)=x2-lnx-a,则G(x)的定义域为(0,+∞),
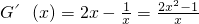 ,
, ,
,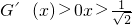
所以G(x)在 上单调递减,在
上单调递减,在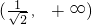 上单调递增 …(10分)
上单调递增 …(10分)
G(x)min=
所以a的取值范围是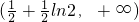 …(12分)
…(12分)
分析:(I)求导,令导数大于零,对a分情况讨论,根据一元二次不等式的解的情况,即可求得结论;
(II)关于x的方程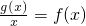 恰有两个不等的实根,等价于G(x)=x2-lnx-a有零点,利用导数工具,将问题转化为求函数的最值问题,即可求得结论.
恰有两个不等的实根,等价于G(x)=x2-lnx-a有零点,利用导数工具,将问题转化为求函数的最值问题,即可求得结论.
点评:掌握导数与函数单调性的关系,会熟练运用导数解决函数的极值与最值问题.考查了计算能力和分析解决问题的能力,体现了分类讨论和转化的数学思想.
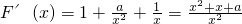 …(1分)
…(1分)①当a≥0时,F'(x)>0,F(x)的单调增区间为(0,+∞),无单调减区间 …(3分)
②当a<0时,方程x2+x+a=0的两根为
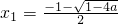 ,
,
当
 时,F'(x)<0
时,F'(x)<0当
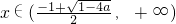 时,F'(x)>0
时,F'(x)>0综上所述,a≥0时,F(x)的单调增区间为(0,+∞),无单调减区间a<0时,F(x)的单调增区间为
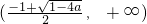 ,单调减区间为
,单调减区间为 …(6分)
…(6分)(Ⅱ)
 …(7分)
…(7分)令G(x)=x2-lnx-a,则G(x)的定义域为(0,+∞),
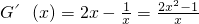 ,
, ,
,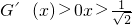
所以G(x)在
 上单调递减,在
上单调递减,在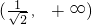 上单调递增 …(10分)
上单调递增 …(10分)G(x)min=

所以a的取值范围是
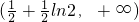 …(12分)
…(12分)分析:(I)求导,令导数大于零,对a分情况讨论,根据一元二次不等式的解的情况,即可求得结论;
(II)关于x的方程
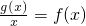 恰有两个不等的实根,等价于G(x)=x2-lnx-a有零点,利用导数工具,将问题转化为求函数的最值问题,即可求得结论.
恰有两个不等的实根,等价于G(x)=x2-lnx-a有零点,利用导数工具,将问题转化为求函数的最值问题,即可求得结论.点评:掌握导数与函数单调性的关系,会熟练运用导数解决函数的极值与最值问题.考查了计算能力和分析解决问题的能力,体现了分类讨论和转化的数学思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目