题目内容
(本小题满分12分)已知椭圆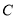 :
: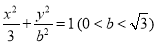 ,其通径(过焦点且与x轴垂直的直线被椭圆截得的线段)长
,其通径(过焦点且与x轴垂直的直线被椭圆截得的线段)长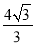 .
.
(1)求椭圆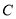 的方程;
的方程;
(2)设过椭圆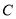 右焦点的直线(不与
右焦点的直线(不与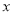 轴重合)与椭圆交于
轴重合)与椭圆交于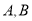 两点,问在
两点,问在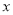 轴上是否存在一点
轴上是否存在一点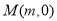 ,使
,使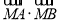 为常数?若存在,求点
为常数?若存在,求点 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
(1) ;(2)存在,且
;(2)存在,且 .
.
【解析】
试题分析:(1)本题是求椭圆的标准方程,而且只要求一个参数 的值,题中已知通径长
的值,题中已知通径长 ,因此解题关键是把通径长用
,因此解题关键是把通径长用 表示出来,只要把通径端点的横坐标
表示出来,只要把通径端点的横坐标 代入椭圆标准方程求得通径长为
代入椭圆标准方程求得通径长为 即可;(2)本小题是直线与椭圆相交的计算问题,一般方法是相交弦的两个端点的坐标为
即可;(2)本小题是直线与椭圆相交的计算问题,一般方法是相交弦的两个端点的坐标为 ,设直线方程为
,设直线方程为 ,把直线方程代入椭圆方程
,把直线方程代入椭圆方程 ,再利用韦达定理表示出
,再利用韦达定理表示出 ,另外计算出
,另外计算出


 ,它是常数与
,它是常数与 无关,则有
无关,则有 ,从而求得
,从而求得 ,还要注意验证当
,还要注意验证当 轴时,也有
轴时,也有 .
.
试题解析:(1)
(2)存在, ,当直线与
,当直线与 轴不垂直时,设
轴不垂直时,设 ,直线的方程为:
,直线的方程为:
代入 得
得





当 时,即
时,即 ,
,
当直线与 轴垂直时,
轴垂直时, ,
,
 ,
,
 .
.
考点:1.椭圆的标准方程;2.直线与椭圆的位置关系.

练习册系列答案
相关题目
 满足
满足 ,则称数列
,则称数列 中,
中, ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中 为正整数.
为正整数. 是“平方递推数列”,且数列
是“平方递推数列”,且数列 为等比数列;
为等比数列; ,即
,即 ,求数列
,求数列 ,求数列
,求数列 的前
的前 ,并求使
,并求使 的
的 ,
, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 满足
满足 ,则
,则 的最小值为( )
的最小值为( ) B.2 C.
B.2 C. D.
D.
 ,集合
,集合 ,
, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 成等差数列,则cos C的最小值是_____.
成等差数列,则cos C的最小值是_____. 满足
满足 ,若
,若
 取得的最优解
取得的最优解 有无数个,则
有无数个,则 的值为( )
的值为( ) B.
B. C.
C.
 成等差数列,则cos C的最小值是_____.
成等差数列,则cos C的最小值是_____. 为接下来被邀请到的6个人中接受挑战的人数,求
为接下来被邀请到的6个人中接受挑战的人数,求