题目内容
【题目】已知数列{an}满足a1=3,a2![]() ,且2an+1=3an﹣an-1.
,且2an+1=3an﹣an-1.
(1)求证:数列{an+1﹣an}是等比数列,并求数列{an}通项公式;
(2)求数列{nan}的前n项和为Tn,若![]() 对任意的正整数n恒成立,求k的取值范围.
对任意的正整数n恒成立,求k的取值范围.
【答案】(1)证明见解析;![]() ;(2)
;(2)![]() .
.
【解析】
(1)由2an+1=3an﹣an-1得![]() ,又a2﹣a1
,又a2﹣a1![]() ,则数列{an+1﹣an}是等比数列,进而求出其通项公式;
,则数列{an+1﹣an}是等比数列,进而求出其通项公式;
(2)根据(1)中求得的结果,先求出nan,再利用错位相减法求前n项和Tn,然后求出k的取值范围.
(1)证明:∵2an+1=3an﹣an-1,∴![]() ,
,
又a2﹣a1![]() ,∴数列{an+1﹣an}是首项为
,∴数列{an+1﹣an}是首项为![]() ,公比为
,公比为![]() 的等比数列.
的等比数列.
∴![]() ,
,
即a2﹣a1![]() ,a3﹣a2
,a3﹣a2![]() ,…,an﹣an-1
,…,an﹣an-1![]() (
(![]() ).
).
等式两边同时相加得an-a1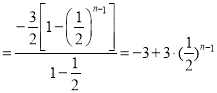 (
(![]() ),
),
则![]() ,
,
又n=1也适合上式,
∴![]() .
.
(2)∵![]() ①,
①,
∴![]() ②,
②,
由①﹣②得
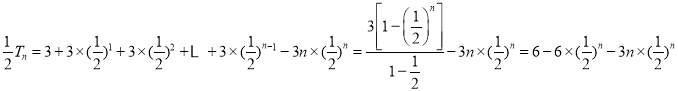
∴![]() ,
,
又![]() ,即
,即![]() ,
,
∴![]() ,
,
令 ![]() ,
,
由![]() ,
,
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
∴![]() ,
,
![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目