题目内容
(12分)已知向量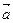 =(cos
=(cos x,sin
x,sin x),
x),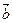 =(cos
=(cos ,sin
,sin )(0
)(0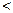

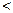
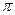 ).
).
设函数f(x)=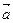 ·
·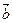 ,且f(x)+
,且f(x)+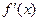 为偶函数. (1)求
为偶函数. (1)求 的值;
的值;
(2)求f(x)的单调增区间.
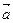 =(cos
=(cos x,sin
x,sin x),
x),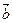 =(cos
=(cos ,sin
,sin )(0
)(0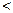

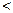
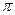 ).
).设函数f(x)=
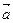 ·
·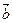 ,且f(x)+
,且f(x)+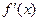 为偶函数. (1)求
为偶函数. (1)求 的值;
的值;(2)求f(x)的单调增区间.
(1) (2)
(2)
 (2)
(2)
(1)因为f(x)=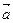 ·
·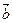 = cos
= cos x cos
x cos +si
+si n
n x sin
x sin = cos(
= cos( x-
x- ),
),
所以f(x)+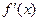 = cos(
= cos( x-
x- )-
)- sin(
sin( x-
x- )="2" cos(
)="2" cos( x-
x- +
+ ),而f(x)+
),而f(x)+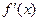 为偶函数,则有-
为偶函数,则有- +
+ = k
= k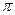 ,k
,k Z,
Z, 又0
又0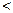

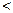
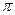 ,则k=0,即
,则k=0,即 =
= ;
;
(2)由(1)得f(x)= c os(
os( x-
x- ),由2k
),由2k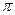 -
-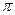

 x-
x-
 2k
2k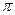 ,解得
,解得 (2k
(2k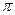 -
- )
) x
x
 (2k
(2k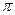 +
+ ),
),
即此函数的单调增区间为 (k
(k Z).
Z).
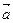 ·
·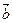 = cos
= cos x cos
x cos +si
+si n
n x sin
x sin = cos(
= cos( x-
x- ),
),所以f(x)+
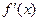 = cos(
= cos( x-
x- )-
)- sin(
sin( x-
x- )="2" cos(
)="2" cos( x-
x- +
+ ),而f(x)+
),而f(x)+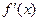 为偶函数,则有-
为偶函数,则有- +
+ = k
= k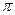 ,k
,k Z,
Z, 又0
又0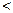

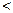
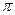 ,则k=0,即
,则k=0,即 =
= ;
;(2)由(1)得f(x)= c
 os(
os( x-
x- ),由2k
),由2k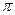 -
-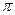

 x-
x-
 2k
2k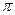 ,解得
,解得 (2k
(2k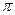 -
- )
) x
x
 (2k
(2k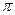 +
+ ),
),即此函数的单调增区间为
 (k
(k Z).
Z).
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
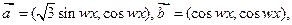 (其中
(其中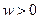 ).设
).设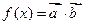 ,且
,且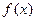 的最小正周期为
的最小正周期为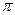 . (1)求
. (1)求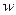 ; (2)若
; (2)若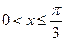 ,求
,求 的图象,只需把
的图象,只需把 的图象
的图象 个单位
个单位 个单位
个单位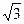 cosx的图象沿x轴向右平移a个单位长度(a
cosx的图象沿x轴向右平移a个单位长度(a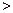 0),所得图象关于y轴对称,则a的最小值为 ( )
0),所得图象关于y轴对称,则a的最小值为 ( )



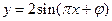 ,x∈R,(其中
,x∈R,(其中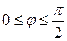 )的图象与y轴交于点(0,1).
)的图象与y轴交于点(0,1). 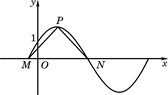
 的值;
的值;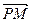 与
与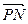 夹角的余弦值.
夹角的余弦值.


 ,
, ]
] (A>0,ω>0)在x=1处取最大值,则 ( )
(A>0,ω>0)在x=1处取最大值,则 ( ) 一定是奇函数
一定是奇函数 一定是奇函数
一定是奇函数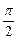 +x)是( )
+x)是( ) ,且
,且 则
则 ___________。
___________。