题目内容
（2013•成都二模）已知G为△ABC的重心，△ABC所在平面内一点P满足2
+2
=
，则
的值等于
．
| PB |
| PC |
| AP |
| ||||||
|
| 6 |
| 5 |
| 6 |
| 5 |
分析：画出图形，判断
与2
+2
共线，然后求出BC的中点E与P连线
，与
以及向量
的关系，即可推出
．
| AP |
| PB |
| PC |
| PE |
| AP |
| AE |
| ||||||
|
解答：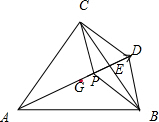
解：如图：因为2
+2
=
，取BC的中点E，显然
与2
+2
共线，2
=4
，
所以
=4
，
+
=
=
，即
=
因为G为△ABC的重心，所以
=
，
所以
=
=
．
故答案为：
解：如图：因为2| PB |
| PC |
| AP |
| AP |
| PB |
| PC |
| PD |
| PE |
所以
| AP |
| PE |
| AP |
| PE |
| AE |
| 5 |
| 4 |
| AP |
| AP |
| 4 |
| 5 |
| AE |
因为G为△ABC的重心，所以
| AG |
| 2 |
| 3 |
| AE |
所以
| ||||||
|
| ||||||||
|
| 6 |
| 5 |
故答案为：
| 6 |
| 5 |
点评：本题给出△ABC中点P满足的向量式，求
的值．着重考查了三角形的中位线定理、平行线的性质和向量的线性运算法则等知识，属于中档题．
| ||
|
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
（2013•成都二模）一个几何体的三视图如图所示，其中正视图是一个正三角形，则该几何体的体积为（ ）