题目内容
已知函数 .
.
(1)求函数f(x)的最小正周期,最大值及取最大值时相应的x值;
(2)如果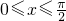 ,求f(x)的取值范围.
,求f(x)的取值范围.
解:(1)f(x)=2sinx( cosx-
cosx- sinx)+
sinx)+ sinxcosx+cos2x
sinxcosx+cos2x
=2 sinxcosx+cos2x-sin2x
sinxcosx+cos2x-sin2x
= sin2x+cos2x
sin2x+cos2x
=2sin(2x+ )…(6分)
)…(6分)
∴f(x)的最小正周期T= =π.
=π.
当2x+ =2kπ+
=2kπ+ ,x=kπ+
,x=kπ+ (k∈z)时,f(x)取得最大值2.…(10分)
(k∈z)时,f(x)取得最大值2.…(10分)
(2)由0≤x≤ ,得
,得 ≤2x+
≤2x+ ≤
≤ ,
,
- ≤sin(2x+
≤sin(2x+ )≤1,
)≤1,
∴f(x)的值域为[-1,2]…(14分)
分析:(1)利用三角函数的倍角公式与辅助角公式将f(x)转化为f(x)=2sin(2x+ ),即可求得函数f(x)的最小正周期,最大值及取最大值时相应的x值;
),即可求得函数f(x)的最小正周期,最大值及取最大值时相应的x值;
(2)由0≤x≤ 可求得
可求得 ≤2x+
≤2x+ ≤
≤ ,利用正弦函数的性质即可求得f(x)的取值范围.
,利用正弦函数的性质即可求得f(x)的取值范围.
点评:本题考查三角函数中的恒等变换应用,考查正弦函数的性质,考查转化与运算能力,属于中档题.
 cosx-
cosx- sinx)+
sinx)+ sinxcosx+cos2x
sinxcosx+cos2x=2
 sinxcosx+cos2x-sin2x
sinxcosx+cos2x-sin2x=
 sin2x+cos2x
sin2x+cos2x=2sin(2x+
 )…(6分)
)…(6分)∴f(x)的最小正周期T=
 =π.
=π.当2x+
 =2kπ+
=2kπ+ ,x=kπ+
,x=kπ+ (k∈z)时,f(x)取得最大值2.…(10分)
(k∈z)时,f(x)取得最大值2.…(10分)(2)由0≤x≤
 ,得
,得 ≤2x+
≤2x+ ≤
≤ ,
,-
 ≤sin(2x+
≤sin(2x+ )≤1,
)≤1,∴f(x)的值域为[-1,2]…(14分)
分析:(1)利用三角函数的倍角公式与辅助角公式将f(x)转化为f(x)=2sin(2x+
 ),即可求得函数f(x)的最小正周期,最大值及取最大值时相应的x值;
),即可求得函数f(x)的最小正周期,最大值及取最大值时相应的x值;(2)由0≤x≤
 可求得
可求得 ≤2x+
≤2x+ ≤
≤ ,利用正弦函数的性质即可求得f(x)的取值范围.
,利用正弦函数的性质即可求得f(x)的取值范围.点评:本题考查三角函数中的恒等变换应用,考查正弦函数的性质,考查转化与运算能力,属于中档题.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目





 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。 .
. 上的函数值的取值范围.
上的函数值的取值范围. .
. 上的函数值的取值范围.
上的函数值的取值范围.