题目内容
已知函数f（x）=
x2-mlnx+（m-1）x，m∈R．（1）若函数f（x）在x=2处取得极值，求m的值；
（2）当m=-2时，讨论函数f（x）+x的单调性；
（3）在（2）的条件下，求证，对任意x1，x2∈（0，+∞）且x1≠x2，有
＞-1．
【答案】分析：（1）由x=2是函数的一个极值点，可得到x=2是f′（x）=0的根，从而求出m；
（2）函数f（x）的定义域为（0，+∞），我们可以构造辅助函数g（x）=f（x）+x，判断g′（x）的符号，进而得到f（x）+x的单调区间；
（3）当 m=-2时，对任意的 x1，x2∈（0，+∞），且x1≠x2，要证明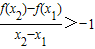
，
即证明f（x1）-f（x2）＞x1-x2，即证f（x1）+x1＜f（x2）+x2，
故我们可由（2）函数g（x）=f（x）+x的单调性，来证明结论．
解答：解：（1）∵函数 f（x）在x=2处有极值∴f′（2）=2-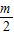
+m-1=0
∴m=-2，经检验m=-2符合题意．∴m=-2．
（2）当m=-2时，函数f（x）=
x2+2lnx-3x（x＞0）．
令函数g（x）=f（x）+x，则
g′（x）=x+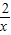
-2=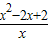
=
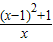
∴g′（x）＞0，即g（x）在（0，+∞）上为增函数．
（3）由（2）知g（x）在（0，+∞）为增函数．
∴对任意0＜x1＜x2，都有g（x1）＜g（x2）成立，
即f（x1）+x1＜f（x2）+x2．
即f（x1）-f（x2）＞x1-x2．
又∵x1-x2＜0，
∴
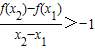（14分）
点评：本题考查导数的综合应用，函数单调性的求法．解题时要认真审题，仔细解答，注意等价转化思想和分类讨论思想的合理运用．
（2）函数f（x）的定义域为（0，+∞），我们可以构造辅助函数g（x）=f（x）+x，判断g′（x）的符号，进而得到f（x）+x的单调区间；
（3）当 m=-2时，对任意的 x1，x2∈（0，+∞），且x1≠x2，要证明
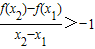，即证明f（x1）-f（x2）＞x1-x2，即证f（x1）+x1＜f（x2）+x2，
故我们可由（2）函数g（x）=f（x）+x的单调性，来证明结论．
解答：解：（1）∵函数 f（x）在x=2处有极值∴f′（2）=2-
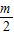+m-1=0∴m=-2，经检验m=-2符合题意．∴m=-2．
（2）当m=-2时，函数f（x）=
x2+2lnx-3x（x＞0）．令函数g（x）=f（x）+x，则
g′（x）=x+
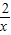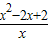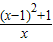
-2==∴g′（x）＞0，即g（x）在（0，+∞）上为增函数．
（3）由（2）知g（x）在（0，+∞）为增函数．
∴对任意0＜x1＜x2，都有g（x1）＜g（x2）成立，
即f（x1）+x1＜f（x2）+x2．
即f（x1）-f（x2）＞x1-x2．
又∵x1-x2＜0，
∴
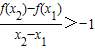（14分）点评：本题考查导数的综合应用，函数单调性的求法．解题时要认真审题，仔细解答，注意等价转化思想和分类讨论思想的合理运用．
练习册系列答案
课堂全解字词句段篇章系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|