题目内容
（1）求证：若x＞0，则ln（1+x）＞
；
（2）若a，b＞0求证：lna-lnb≥1-
．
| x |
| 1+x |
（2）若a，b＞0求证：lna-lnb≥1-
| b |
| a |
（1）f（x）=ln（1+x）-
，∴f′（x）=
x＞0时f′（x）＞0，在（0，+∞）上是增函数．
∴x＞0时，f（x）＞f（0）=0，∴ln（1+x）＞
（2）令f（x）=ln（1+x）-
，
由（1），f（x）在x=0处取得最小值．
即ln（1+x）-
≥0
∴而lna-lnb-1+
=ln
+
-1=f（
-1)
∴lna-lnb-1+
≥0
即lna-lnb≥1-
．
| x |
| 1+x |
| x |
| (1+x) 2 |
x＞0时f′（x）＞0，在（0，+∞）上是增函数．
∴x＞0时，f（x）＞f（0）=0，∴ln（1+x）＞
| x |
| 1+x |
（2）令f（x）=ln（1+x）-
| x |
| 1+x |
由（1），f（x）在x=0处取得最小值．
即ln（1+x）-
| x |
| 1+x |
∴而lna-lnb-1+
| b |
| a |
| a |
| b |
| b |
| a |
| a |
| b |
∴lna-lnb-1+
| b |
| a |
即lna-lnb≥1-
| b |
| a |
练习册系列答案
名校课堂系列答案
相关题目
；
．
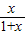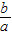