题目内容
已知函数 .
.
(1)求f(0);
(2)探究f(x)的单调性,并证明你的结论;
(3)若f(x)为奇函数,求满足f(ax)<f(2)的x的范围.
解:(1)f(0)= .
.
(2)∵f(x)的定义域为R∴任取x1x2∈R且x1<x2
则 =
=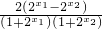 .
.
∵y=2x在R是单调递增且x1<x2
∴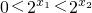
∴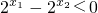
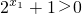
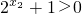
∴f(x1)-f(x2)<0
即f(x1)<f(x2),
∴f(x)在R上单调递增.
(3)∵f(x)是奇函数∴f(-x)=-f(x),
即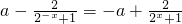 ,
,
解得:a=1.
∴f(ax)<f(2)
即为f(x)<f(2)
又∵f(x)在R上单调递增
∴x<2.
分析:(1)直接代入即可获得解答;
(2)根据函数单调性的定义,首先应在所给区间上任设两个数并规定大小,然后通过作差法分析获得两数对应函数值之间的大小关系即可;
(3)充分利用好函数的奇偶性,即可求的a的值,从而将问题简化为满足f(x)<f(2)求x的取值范围,结合函数的单调性即可获得问题的解答.
点评:本题考查的是函数单调性、奇偶性等知识的综合问题.在解答的过程当中充分体现了计算的能力、单调性定义的应用以及问题转化的能力.值得同学们体会和反思.
 .
.(2)∵f(x)的定义域为R∴任取x1x2∈R且x1<x2
则
 =
=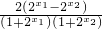 .
.∵y=2x在R是单调递增且x1<x2
∴
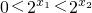
∴
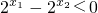
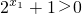
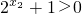
∴f(x1)-f(x2)<0
即f(x1)<f(x2),
∴f(x)在R上单调递增.
(3)∵f(x)是奇函数∴f(-x)=-f(x),
即
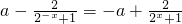 ,
,解得:a=1.
∴f(ax)<f(2)
即为f(x)<f(2)
又∵f(x)在R上单调递增
∴x<2.
分析:(1)直接代入即可获得解答;
(2)根据函数单调性的定义,首先应在所给区间上任设两个数并规定大小,然后通过作差法分析获得两数对应函数值之间的大小关系即可;
(3)充分利用好函数的奇偶性,即可求的a的值,从而将问题简化为满足f(x)<f(2)求x的取值范围,结合函数的单调性即可获得问题的解答.
点评:本题考查的是函数单调性、奇偶性等知识的综合问题.在解答的过程当中充分体现了计算的能力、单调性定义的应用以及问题转化的能力.值得同学们体会和反思.

练习册系列答案
相关题目
 .
. .
. 的图象在x轴上方?
的图象在x轴上方? .
. 为f(x)的一个零点,求sin2x的值.
为f(x)的一个零点,求sin2x的值.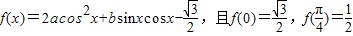 .
. .
. ,求f(x)的最大值和最小值.
,求f(x)的最大值和最小值.