题目内容
双曲线C1:x2-
=1的一条渐近线与椭圆C2:
+
=1相交于点P,若|OP|=2,则椭圆C2的离心率为( )
| y2 |
| 3 |
| x2 |
| a2 |
| y2 |
| a2-4 |
分析:先根据双曲线C1:x2-
=1,得出它的一条渐近线方程为:y=
x,其倾斜角为60°,从而得到∠POx=60°又|OP|=2,故可得P点的坐标,将P的坐标代入椭圆方程得a从而求出椭圆C2的离心率.
| y2 |
| 3 |
| 3 |
解答:解:根据双曲线C1:x2-
=1,得出它的一条渐近线方程为:y=
x,其倾斜角为60°,
设这条渐近线与椭圆C2:
+
=1相交于点P,
则∠POx=60°且|OP|=2,故可得P点的坐标为(1,
).
代入椭圆方程得:
+
=1,⇒a=
+1或a=
-1<2(不合,舍去)
∴椭圆C2:
+
=1的a=
+1,b2=2
,
∴c=
=2,
则椭圆C2的离心率为
=
=
-1.
故选A.
| y2 |
| 3 |
| 3 |
设这条渐近线与椭圆C2:
| x2 |
| a2 |
| y2 |
| a2-4 |
则∠POx=60°且|OP|=2,故可得P点的坐标为(1,
| 3 |
代入椭圆方程得:
| 12 |
| a2 |
(
| ||
| a2-4 |
| 3 |
| 3 |
∴椭圆C2:
| x2 |
| a2 |
| y2 |
| a2-4 |
| 3 |
| 3 |
∴c=
| a2-b2 |
则椭圆C2的离心率为
| c |
| a |
| 2 | ||
|
| 3 |
故选A.
点评:本小题主要考查椭圆的简单性质、双曲线的简单性质等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
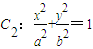 有公共焦点F1F2,点
有公共焦点F1F2,点 是它们的一个公共点.
是它们的一个公共点.