题目内容
设函数 .
.(1)求f(x)的最大值及周期;
(2)若锐角α满足
 ,求
,求 的值.
的值.
【答案】分析:(1)函数解析式利用二倍角的正弦、余弦函数公式化简,再利用两角和与差的余弦函数公式化为一个角的余弦函数,根据余弦函数的图象与性质求出f(x)的最大值以及周期即可;
(2)根据f(α)=3-2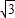 ,求出α的值,代入所求式子中计算即可求出值.
,求出α的值,代入所求式子中计算即可求出值.
解答:解:(1)f(x)=6×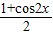 -
-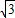 sin2x=3cos2x-
sin2x=3cos2x-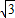 sin2x+3=2
sin2x+3=2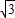 cos(2x+
cos(2x+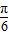 )+3,
)+3,
当2x+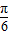 =2kπ,k∈Z,即x=-
=2kπ,k∈Z,即x=-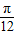 +kπ,k∈Z时,f(x)取得最大值,最大值为2
+kπ,k∈Z时,f(x)取得最大值,最大值为2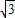 +3,
+3,
∵ω=2,∴T=π;
(2)∵锐角α满足f(α)=3-2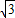 ,
,
∴2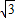 cos(2α+
cos(2α+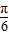 )+3=3-2
)+3=3-2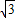 ,即cos(2α+
,即cos(2α+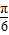 )=-1,
)=-1,
∴2α+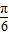 =π,即α=
=π,即α=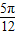 ,
,
则tan α=tan
α=tan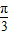 =
=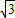 .
.
点评:此题考查了二倍角的正弦、余弦函数公式,以及两角和与差的余弦函数公式,熟练掌握公式是解本题的关键.
(2)根据f(α)=3-2
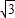 ,求出α的值,代入所求式子中计算即可求出值.
,求出α的值,代入所求式子中计算即可求出值.解答:解:(1)f(x)=6×
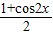 -
-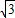 sin2x=3cos2x-
sin2x=3cos2x-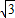 sin2x+3=2
sin2x+3=2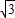 cos(2x+
cos(2x+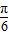 )+3,
)+3,当2x+
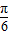 =2kπ,k∈Z,即x=-
=2kπ,k∈Z,即x=-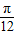 +kπ,k∈Z时,f(x)取得最大值,最大值为2
+kπ,k∈Z时,f(x)取得最大值,最大值为2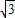 +3,
+3,∵ω=2,∴T=π;
(2)∵锐角α满足f(α)=3-2
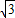 ,
,∴2
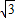 cos(2α+
cos(2α+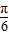 )+3=3-2
)+3=3-2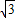 ,即cos(2α+
,即cos(2α+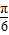 )=-1,
)=-1,∴2α+
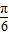 =π,即α=
=π,即α=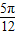 ,
,则tan
 α=tan
α=tan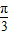 =
=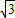 .
.点评:此题考查了二倍角的正弦、余弦函数公式,以及两角和与差的余弦函数公式,熟练掌握公式是解本题的关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
 .
. ,求
,求 的值.
的值. .
.
 时,求sin2x.
时,求sin2x. .
. ,c=3,求a的值.
,c=3,求a的值.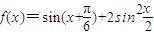 .
. ,求b值.
,求b值.