题目内容
已知点(1,
)是函数f(x)=ax(a>0且a≠1)的图象上一点,等比数列{an}的前n项和为f(n)-c,数列{bn}(bn>0)的首项为c,且前n项和Sn满足Sn-Sn-1=
+
(n≥2)
(Ⅰ)求数列{an}和{bn}的通项公式
(Ⅱ)求数列{
}前n项和为Tn.
| 1 |
| 3 |
| Sn |
| Sn-1 |
(Ⅰ)求数列{an}和{bn}的通项公式
(Ⅱ)求数列{
| 1 |
| bnbn+1 |
(Ⅰ)∵f(1)=
,故a=
,
∴f(x)=(
)x,
∵a1=f(1)-c=
-c,a2=[f(2)-c]-[f(1)-c]=-
,a3=[f(3)-c]-[f(2)-c]=-
,
又数列{an}为等比数列,a1=
=
=-
=
-c,
∴c=1,又公比q=
=
,
∴an=-
(
)n-1=-2(
)n,n∈N*;
∵Sn-Sn-1=(
+
)(
-
)=
+
(n≥2),
又bn>0,
>0,
∴
-
=1;
∴数列{
}构成一个首相为1公差为1的等差数列,
∴
=1+(n-1)×1=n,于是Sn=n2;
当n≥2,bn=Sn-Sn-1=n2-(n-1)2=2n-1;
∴bn=2n-1,n∈N*;
(Ⅱ)∵
=
=
(
-
),
∴Tn=
+
+…+
=
[(1-
)+(
-
)+(
-
)+(
-
)+…+(
-
)]
=
(1-
)
=
.
| 1 |
| 3 |
| 1 |
| 3 |
∴f(x)=(
| 1 |
| 3 |
∵a1=f(1)-c=
| 1 |
| 3 |
| 2 |
| 9 |
| 2 |
| 27 |
又数列{an}为等比数列,a1=
| a22 |
| a3 |
| ||
-
|
| 2 |
| 3 |
| 1 |
| 3 |
∴c=1,又公比q=
| a2 |
| a1 |
| 1 |
| 3 |
∴an=-
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∵Sn-Sn-1=(
| Sn |
| Sn-1 |
| Sn |
| Sn-1 |
| Sn |
| Sn-1 |
又bn>0,
| Sn |
∴
| Sn |
| Sn-1 |
∴数列{
| Sn |
∴
| Sn |
当n≥2,bn=Sn-Sn-1=n2-(n-1)2=2n-1;
∴bn=2n-1,n∈N*;
(Ⅱ)∵
| 1 |
| bnbn+1 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴Tn=
| 1 |
| b1b2 |
| 1 |
| b2b3 |
| 1 |
| bnbn+1 |
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 7 |
| 1 |
| 9 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=
| 1 |
| 2 |
| 1 |
| 2n+1 |
=
| n |
| 2n+1 |

练习册系列答案
相关题目
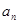 }中,
}中,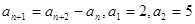 ,则
,则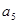 为___________.
为___________.