题目内容
已知全集U=R.P={x|a+1≤x≤2a+1},Q={x|-2≤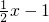 ≤
≤ }
}
(1)若a=3,求(CUP)∩Q;
(2)若P⊆Q,求实数a的取值范围.
解:(1)若a=3,则P={x|4≤x≤7},
∴(CUP)={x}x<4,或 x>7}.又Q={x|-2≤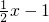 ≤
≤ }={x|-2≤x≤5 },
}={x|-2≤x≤5 },
∴(CUP)∩Q=[-2,4).…(4分)
(2)解:∵P⊆Q,P={x|a+1≤x≤2a+1},Q={x|-2≤x≤5 },
当 P=∅时,由a+1>2a+1 解得:a<0.…(6分)
当P≠∅时,由 解得:0≤a≤2.
解得:0≤a≤2.
综上所述:a的取值范围为(-∞,2].…(10分)
分析:(1)先根据补集的定义求得CUP,再根据交集的定义求得(CUP)∩Q.
(2)当 P=∅时,由a+1>2a+1 解得a的范围,当P≠∅时,由 解得 a 的范围.再把这两个a 的范围 取并集,即得所求.
解得 a 的范围.再把这两个a 的范围 取并集,即得所求.
点评:本题主要考查集合关系中参数的取值范围问题,两个集合的交集、补集的定义和求法,体现了分类讨论的数学思想,属于基础题.
∴(CUP)={x}x<4,或 x>7}.又Q={x|-2≤
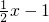 ≤
≤ }={x|-2≤x≤5 },
}={x|-2≤x≤5 },∴(CUP)∩Q=[-2,4).…(4分)
(2)解:∵P⊆Q,P={x|a+1≤x≤2a+1},Q={x|-2≤x≤5 },
当 P=∅时,由a+1>2a+1 解得:a<0.…(6分)
当P≠∅时,由
 解得:0≤a≤2.
解得:0≤a≤2.综上所述:a的取值范围为(-∞,2].…(10分)
分析:(1)先根据补集的定义求得CUP,再根据交集的定义求得(CUP)∩Q.
(2)当 P=∅时,由a+1>2a+1 解得a的范围,当P≠∅时,由
 解得 a 的范围.再把这两个a 的范围 取并集,即得所求.
解得 a 的范围.再把这两个a 的范围 取并集,即得所求.点评:本题主要考查集合关系中参数的取值范围问题,两个集合的交集、补集的定义和求法,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ( )
( ) B.
B.
 D.
D.


 B.
B. C.
C. D.
D. 
 ≤
≤ }
}