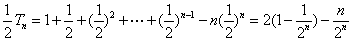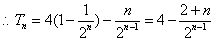题目内容
数列 首项
首项 ,前
,前 项和
项和 满足等式
满足等式 (常数
(常数 ,
, ……)
……)
(1)求证: 为等比数列;
为等比数列;
(2)设数列 的公比为
的公比为 ,作数列
,作数列 使
使 (
( …),求数列
…),求数列 的通项公式.
的通项公式.
(3)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
(1)由 得
得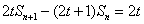
两式相减得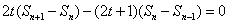
故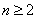 时,
时,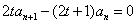
从而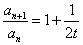
又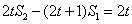 即
即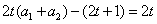 ,而
,而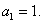
从而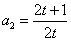 故
故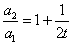
 对任意
对任意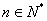 ,
,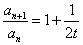 为常数,即
为常数,即 为等比数列
为等比数列
(2)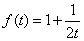
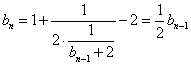 …
…
又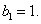 故
故 为等比数列,通项公式为
为等比数列,通项公式为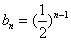
(3)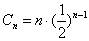
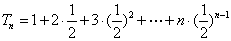 两边同乘以
两边同乘以
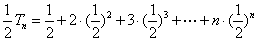
两式相减得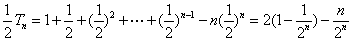
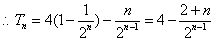

练习册系列答案
相关题目
题目内容
数列 首项
首项 ,前
,前 项和
项和 满足等式
满足等式 (常数
(常数 ,
, ……)
……)
(1)求证: 为等比数列;
为等比数列;
(2)设数列 的公比为
的公比为 ,作数列
,作数列 使
使 (
( …),求数列
…),求数列 的通项公式.
的通项公式.
(3)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
(1)由 得
得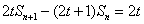
两式相减得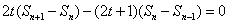
故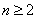 时,
时,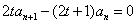
从而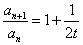
又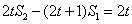 即
即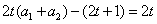 ,而
,而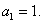
从而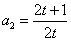 故
故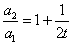
 对任意
对任意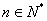 ,
,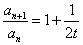 为常数,即
为常数,即 为等比数列
为等比数列
(2)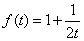
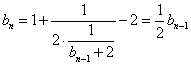 …
…
又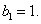 故
故 为等比数列,通项公式为
为等比数列,通项公式为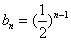
(3)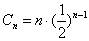
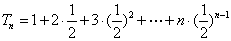 两边同乘以
两边同乘以
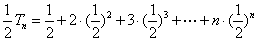
两式相减得