题目内容
【题目】已知双曲线![]() (b>a>0),O为坐标原点,离心率
(b>a>0),O为坐标原点,离心率![]() ,点
,点![]() 在双曲线上.
在双曲线上.
(1)求双曲线的方程;
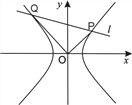
(2)若直线![]() 与双曲线交于P、Q两点,且
与双曲线交于P、Q两点,且![]() .求|OP|2+|OQ|2的最小值.
.求|OP|2+|OQ|2的最小值.
【答案】![]() 1
1![]()
![]() ;
;![]() 2
2![]() .
.
【解析】试题分析:
(Ⅰ) 由![]() ,可得
,可得![]() ,故双曲线方程为
,故双曲线方程为![]() ,代入点
,代入点![]() 的坐标可得
的坐标可得![]() ,由此可得双曲线方程. (Ⅱ)根据直线
,由此可得双曲线方程. (Ⅱ)根据直线![]() 的斜率存在与否分两种情况求解.当斜率存在时,可根据一元二次方程根与系数的关系及两点间的距离公式求解即可.当斜率不存在时直接计算可得结果.
的斜率存在与否分两种情况求解.当斜率存在时,可根据一元二次方程根与系数的关系及两点间的距离公式求解即可.当斜率不存在时直接计算可得结果.
试题解析:
(1)由![]() ,可得
,可得![]() ,
,
∴![]() ,
,
∴ 双曲线方程为![]() ,
,
∵ 点![]() 在双曲线上,
在双曲线上,
∴![]() ,
,
解得 ![]() ,
,
∴ 双曲线的方程为![]() .
.
(2)①当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,
由![]() 消去y整理得
消去y整理得![]() ,
,
∵直线![]() 与双曲线交于
与双曲线交于![]() 两点,
两点,
∴![]() .
.
设![]() ,
,![]() ,
,
则![]() ,
,
由![]() 得到:
得到:![]() ,
,
即![]() ,
,
∴![]() ,
,
化简得![]() .
.
∴![]() ,
,
当![]() 时上式取等号,且方程(*)有解.
时上式取等号,且方程(*)有解.
②当直线![]() 的斜率不存在时,设直线
的斜率不存在时,设直线![]() 的方程为
的方程为![]() ,则有
,则有![]() ,
,
由![]() 可得
可得![]() ,
,
可得![]() ,解得
,解得![]() .
.
∴![]() .
.
∴![]()
![]() .
.
综上可得![]() 的最小值是24.
的最小值是24.

练习册系列答案
相关题目