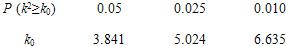题目内容
 =
=
- A.

- B.
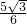
- C.
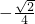
- D.

B
分析:把原式第二项的角75°变形为90°-15°,利用诱导公式化简后,前两项利用二倍角的余弦函数公式及特殊角的三角函数值化简,第三项利用二倍角的正切函数公式及特殊角的三角函数值化简,通分后计算即可得到值.
解答:
=cos215°-cos2(90°-15°)+tan30°
=cos215°-sin215°+tan30°
=cos30°+tan30°
= +
+
=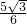 .
.
故选B
点评:此题常考了诱导公式,二倍角的正切、余弦函数公式,以及特殊角的三角函数值,熟练掌握公式是解本题的关键.
分析:把原式第二项的角75°变形为90°-15°,利用诱导公式化简后,前两项利用二倍角的余弦函数公式及特殊角的三角函数值化简,第三项利用二倍角的正切函数公式及特殊角的三角函数值化简,通分后计算即可得到值.
解答:

=cos215°-cos2(90°-15°)+tan30°
=cos215°-sin215°+tan30°
=cos30°+tan30°
=
 +
+
=
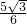 .
.故选B
点评:此题常考了诱导公式,二倍角的正切、余弦函数公式,以及特殊角的三角函数值,熟练掌握公式是解本题的关键.

练习册系列答案
相关题目