题目内容
(2013•朝阳区二模)为提高学生学习数学的兴趣,某地区举办了小学生“数独比赛”.比赛成绩共有90分,70分,60分,40分,30分五种,按本次比赛成绩共分五个等级.从参加比赛的学生中随机抽取了30名学生,并把他们的比赛成绩按这五个等级进行了统计,得到如下数据表:
(Ⅰ)根据上面的统计数据,试估计从本地区参加“数独比赛”的小学生中任意抽取一人,其成绩等级为“A 或B”的概率;
(Ⅱ)根据(Ⅰ)的结论,若从该地区参加“数独比赛”的小学生(参赛人数很多)中任选3人,记X表示抽到成绩等级为“A或B”的学生人数,求X的分布列及其数学期望EX;
(Ⅲ)从这30名学生中,随机选取2人,求“这两个人的成绩之差大于20分”的概率.
| 成绩等级 | A | B | C | D | E |
| 成绩(分) | 90 | 70 | 60 | 40 | 30 |
| 人数(名) | 4 | 6 | 10 | 7 | 3 |
(Ⅱ)根据(Ⅰ)的结论,若从该地区参加“数独比赛”的小学生(参赛人数很多)中任选3人,记X表示抽到成绩等级为“A或B”的学生人数,求X的分布列及其数学期望EX;
(Ⅲ)从这30名学生中,随机选取2人,求“这两个人的成绩之差大于20分”的概率.
分析:(I)本题是一个统计问题,根据统计数据,从而得出从本地区参加“数独比赛”的小学生中任意抽取一人,其成绩等级为“A 或B”的概率得到结果.
(II)由题意知由题意知随机变量X可取0,1,2,3,结合变量对应的事件和等可能事件的概率公式写出变量的概率,写出分布列和做出期望值.
(III)设事件M:从这30名学生中,随机选取2人,这两个人的成绩之差大于20分.设从这30名学生中,随机选取2人,记两个人的成绩分别为m,n.得到基本事件的总数,不妨设m>n,再对m,n的取值情形进行分类讨论算出各自的基本事件数,最后根据概率公式计算即可求得事件M的概率.
(II)由题意知由题意知随机变量X可取0,1,2,3,结合变量对应的事件和等可能事件的概率公式写出变量的概率,写出分布列和做出期望值.
(III)设事件M:从这30名学生中,随机选取2人,这两个人的成绩之差大于20分.设从这30名学生中,随机选取2人,记两个人的成绩分别为m,n.得到基本事件的总数,不妨设m>n,再对m,n的取值情形进行分类讨论算出各自的基本事件数,最后根据概率公式计算即可求得事件M的概率.
解答:解:(I)根据统计数据可知,从本地区参加“数独比赛”的30名小学生中任意抽取一人,其成绩等级为“A 或B”的概率为
+
=
,
即从本地区参加“数独比赛”的小学生中任意抽取一人,其成绩等级为“A 或B”的概率为
.
(II)由题意知随机变量X可取0,1,2,3,
∴P(X=0)=C
(
)0(
)3=
;P(X=1)=C
(
)1(
)2=
;
P(X=2)=C
(
)2(
)=
;
P(X=3)=C
(
)3(
)0=
;
所以X的分布列为(必须写出分布列,否则扣1分)
…(11分)
故Eξ=0×
+1×
+2×
+3×
=1,所求期望值为1.
(III)设事件M:从这30名学生中,随机选取2人,这两个人的成绩之差大于20分.
设从这30名学生中,随机选取2人,记两个人的成绩分别为m,n.
则基本事件的总数为
,
不妨设m>n,
当m=90时,n=60或40或30,基本事件的数为C
(C
+C
+C
);
当m=70时,n=40或30,基本事件的数为C
(C
+C
);
当m=60时,n=30,基本事件的数为C
C
;
∴P(M)=
=
.
∴从这30名学生中,随机选取2人,“这两个人的成绩之差大于20分”的概率为
.
| 4 |
| 30 |
| 6 |
| 30 |
| 1 |
| 3 |
即从本地区参加“数独比赛”的小学生中任意抽取一人,其成绩等级为“A 或B”的概率为
| 1 |
| 3 |
(II)由题意知随机变量X可取0,1,2,3,
∴P(X=0)=C
0 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 8 |
| 27 |
1 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
P(X=2)=C
2 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
P(X=3)=C
3 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 27 |
所以X的分布列为(必须写出分布列,否则扣1分)
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
故Eξ=0×
| 8 |
| 27 |
| 4 |
| 9 |
| 2 |
| 9 |
| 1 |
| 27 |
(III)设事件M:从这30名学生中,随机选取2人,这两个人的成绩之差大于20分.
设从这30名学生中,随机选取2人,记两个人的成绩分别为m,n.
则基本事件的总数为
| C | 2 30 |
不妨设m>n,
当m=90时,n=60或40或30,基本事件的数为C
1 4 |
1 10 |
1 7 |
1 3 |
当m=70时,n=40或30,基本事件的数为C
1 6 |
1 7 |
1 3 |
当m=60时,n=30,基本事件的数为C
1 10 |
1 3 |
∴P(M)=
| ||||||||||||||||||
|
| 34 |
| 87 |
∴从这30名学生中,随机选取2人,“这两个人的成绩之差大于20分”的概率为
| 34 |
| 87 |
点评:本题考查等可能事件的概率,考查相互独立事件同时发生的概率,考查离散型随机变量的分布列和期望,本题是一个典型的综合题目.

练习册系列答案
相关题目
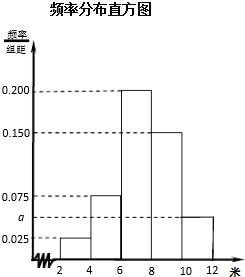 (2013•朝阳区二模)为了解某市今年初二年级男生的身体素质状况,从该市初二年级男生中抽取了一部分学生进行“掷实心球”的项目测试.成绩低于6米为不合格,成绩在6至8米(含6米不含8米)的为及格,成绩在8米至12米(含8米和12米,假定该市初二学生掷实心球均不超过12米)为优秀.把获得的所有数据,分成[2,4),[4,6),[6,8),[8,10),[10,12]五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.
(2013•朝阳区二模)为了解某市今年初二年级男生的身体素质状况,从该市初二年级男生中抽取了一部分学生进行“掷实心球”的项目测试.成绩低于6米为不合格,成绩在6至8米(含6米不含8米)的为及格,成绩在8米至12米(含8米和12米,假定该市初二学生掷实心球均不超过12米)为优秀.把获得的所有数据,分成[2,4),[4,6),[6,8),[8,10),[10,12]五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.