题目内容
[番茄花园1] 有4位同学在同一天的上、下午参加“身高与体重”、“立定跳远”、“肺活量”、“握力”、
“台阶”五个项目的测试，每位同学上、下午各测试一个项目，且不重复. 若上午不测“握
力”项目，下午不测“台阶”项目，其余项目上、下午都各测试一人. 则不同的安排方式共
有______________种（用数字作答）.
[番茄花园1]1.
[番茄花园1] 甲罐中有5个红球，2个白球和3个黑球，乙罐中有4个红球，3个白球和3个黑球.先从甲罐中随机取出一球放入乙罐，分别以
、
和
表示由甲罐取出的球是红球、白球和黑球的事件；再从乙罐中随机取出一球，以
表示由乙罐取出的球是红球的事件.则下列结论中正确的是
(写出所有正确结论的编号)
①
；②
；③事件与事件相互独立；④，，是两两互斥的事件；⑤
的值不能确定，因为它与，，中究竟哪一个发生有关.
[番茄花园1]15.
为调查某地区老人是否需要志愿者提供帮助，用简单随机抽样方法从该地区调查了500位老年人，结果如下：
|
是否需要志愿 性别 |
男 |
女 |
|
需要 |
40 |
30 |
|
不需要 |
160 |
270 |
（1）
（2） 估计该地区老年人中，需要志愿者提供帮助的老年人的比例；
（3） 能否有99％的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关？
（4） 根据（2）的结论，能否提供更好的调查方法来估计该地区老年人，需要志愿帮助的老年人的比例？说明理由
附：
[番茄花园1]1.
设
（
且
），g(x)是f(x)的反函数.
（Ⅰ）设关于
的方程求
在区间[2，6]上有实数解，求t的取值范围；
（Ⅱ）当a＝e（e为自然对数的底数）时，证明：
；
（Ⅲ）当0＜a≤时，试比较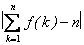
与4的大小，并说明理由.
[番茄花园1]1.
[番茄花园1] 品酒师需定期接受酒味鉴别功能测试，一种通常采用的测试方法如下：拿出
瓶外观相同但品质不同的酒让其品尝，要求其按品质优劣为它们排序；经过一段时间，等其记忆淡忘之后，再让其品尝这瓶酒，并重新按品质优劣为它们排序，这称为一轮测试.根据一轮测试中的两次排序的偏离程度的高低为其评分.
现设
，分别以
，
，
，
表示第一次排序时被排为1，2，3，4的四种酒在第二次排序时的序号，并令
.
则
是对两次排序的偏离程度的一种描述.
(Ⅰ)写出的可能值集合；
(Ⅱ)假设，，，等可能地为1，2，3，4的各种排列，求的分布列；
(Ⅲ)某品酒师在相继进行的三轮测试中，都有
.
(ⅰ)试按(Ⅱ)中的结果，计算出现这种现象的概率(假定各轮测试相互独立)；
(ⅱ)你认为该品酒师的酒味鉴别功能如何？说明理由.
[番茄花园1]21.