题目内容
(本题满分12分)已知函数 ,
, .
.
(1)求函数 的单调递减区间;
的单调递减区间;
(2)求函数 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
(1) ;(2)最大值为
;(2)最大值为 ,最小值为
,最小值为 ;
;
【解析】
试题分析:(1)由题可知,由二倍角公式化简得, ,再由和差化积得到
,再由和差化积得到 ,正弦函数的递减区间为
,正弦函数的递减区间为 ,因此,由不等式
,因此,由不等式 ,解得
,解得 ,则递减区间为
,则递减区间为 ;
;
(2)当 ,
, ,由函数图像知,
,由函数图像知, ,因此,最大值为
,因此,最大值为 ,最小值为
,最小值为 ;
;
试题解析:(1) 
 ∴
∴ ,
,
得 ,则
,则 的递减区间为
的递减区间为 6分
6分
(2)∵ ,∴
,∴ ∴
∴
故函数 在区间
在区间 上的最大值为
上的最大值为 ,最小值为
,最小值为 12分
12分
考点:二倍角公式和差化积的应用三角函数的单调性
考点分析: 考点1:三角函数的图象及性质 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 中,侧棱与底面垂直,
中,侧棱与底面垂直, ,
, ,
, 是
是 的中点,
的中点, 是
是 与
与 的交点.
的交点.
 平面
平面 ;
; 平面
平面 .
. 上一点
上一点 到焦点的距离为
到焦点的距离为 ,那么
,那么 的横坐标是( )
的横坐标是( ) B.
B. C.
C. D.
D.
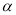 ,
,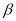 ,
,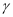 ,且
,且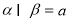 ,
,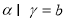 ,
,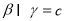 ,给出下列命题:①
,给出下列命题:①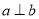 ,
,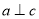 ,则
,则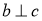 ;
;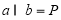 ,则
,则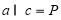 ;
;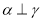 ;
;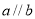 ,则
,则 。
。 的解集是
的解集是 ,则
,则 的值是( )
的值是( ) 的单调递减区间为 .
的单调递减区间为 . ,则
,则 =
= B.
B. C.5 D.
C.5 D.
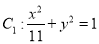 ,双曲线
,双曲线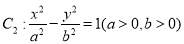 ,若以C1的长轴为直径的圆与C2的一条渐近线交于A,B两点,且C1与该渐近线的两交点将线段AB三等分,则C2的离心率为( )
,若以C1的长轴为直径的圆与C2的一条渐近线交于A,B两点,且C1与该渐近线的两交点将线段AB三等分,则C2的离心率为( )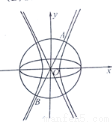
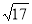 C.
C.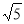 D.
D.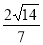
 内任取一个实数
内任取一个实数 ,设
,设 ,则函数
,则函数 的图像与
的图像与 轴有公共点的概率等于 。
轴有公共点的概率等于 。