题目内容
如图所示,长方体ABCD—A′B′C′D′中,用截面截下一个棱锥C—A′DD′,
求棱锥C—A′DD′的体积与剩余部分的体积之比.
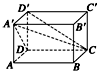
棱锥C—A′DD′的体积与剩余部分的体积之比为1∶5
解析:
已知长方体可以看成直四棱柱ADD′A′—BCC′B′.
设它的底面ADD′A′面积为S,高为h,则它的体积为V=Sh.
而棱锥C—A′DD′的底面面积为![]() S,高是h,
S,高是h,
因此,棱锥C—A′DD′的体积
VC—A′DD′=![]() ×
×![]() Sh=
Sh=![]() Sh.
Sh.
余下的体积是Sh-![]() Sh=
Sh=![]() Sh.
Sh.
所以棱锥C—A′DD′的体积与剩余部分的体积之比为1∶5.

练习册系列答案
相关题目
 如图所示的长方体ABCD-A1B1C1D1中AB=BB1且BC=2AB,E,F分别是BC1,A1D1的中点,则异面直线BE与DF所成的角是
如图所示的长方体ABCD-A1B1C1D1中AB=BB1且BC=2AB,E,F分别是BC1,A1D1的中点,则异面直线BE与DF所成的角是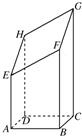 如图所示,以AB=4cm,BC=3cm的长方形ABCD为底面的长方体被平面斜着截断的几何体,EFGH是它的截面.当AE=5cm,BF=8cm,CG=12cm时,试回答下列问题:
如图所示,以AB=4cm,BC=3cm的长方形ABCD为底面的长方体被平面斜着截断的几何体,EFGH是它的截面.当AE=5cm,BF=8cm,CG=12cm时,试回答下列问题:
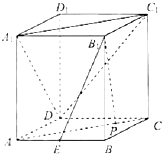 如图所示,长方体ABCD-A1B1C1D1中,P是线段AC上任意一点.
如图所示,长方体ABCD-A1B1C1D1中,P是线段AC上任意一点. ,
, =
= ,则二面角
,则二面角 的大小为_______;
的大小为_______;