题目内容
计算求值:(1)cos
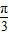 +tan
+tan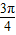 -sin(
-sin(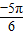 )-sin
)-sin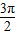
(2)sin
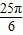 +cos(-
+cos(-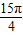 )+tan
)+tan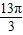 -cos
-cos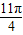 .
.
【答案】分析:利用诱导公式,转化为锐角的三角函数,即可得到结论.
解答:解:(1)原式=cos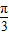 +tan(
+tan(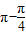 )+sin(π-
)+sin(π-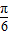 )-sin(π+
)-sin(π+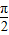 )
)
= -tan
-tan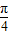 +sin
+sin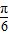 +sin
+sin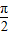
= -1+
-1+ +1
+1
=1
(2)原式=sin(4π+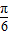 )+cos(
)+cos(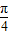 -4π)+tan(
-4π)+tan(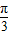 +4π)-cos(3π-
+4π)-cos(3π-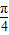 )
)
=sin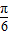 -cos
-cos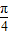 +tan
+tan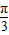 +cos
+cos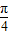
= -
-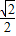 +
+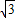 +
+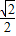
=
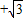
点评:本题考查诱导公式的运用,解题的关键是利用诱导公式,转化为锐角的三角函数,属于基础题.
解答:解:(1)原式=cos
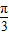 +tan(
+tan(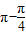 )+sin(π-
)+sin(π-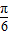 )-sin(π+
)-sin(π+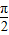 )
)=
 -tan
-tan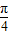 +sin
+sin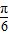 +sin
+sin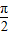
=
 -1+
-1+ +1
+1=1
(2)原式=sin(4π+
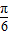 )+cos(
)+cos(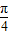 -4π)+tan(
-4π)+tan(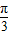 +4π)-cos(3π-
+4π)-cos(3π-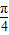 )
)=sin
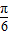 -cos
-cos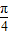 +tan
+tan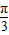 +cos
+cos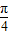
=
 -
-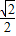 +
+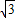 +
+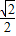
=

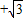
点评:本题考查诱导公式的运用,解题的关键是利用诱导公式,转化为锐角的三角函数,属于基础题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目