题目内容
 如图:已知圆上的弧
如图:已知圆上的弧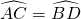 ,过C点的圆的切线与BA的延长线交于E点,证明:
,过C点的圆的切线与BA的延长线交于E点,证明:
(Ⅰ)∠ACE=∠BCD.
(Ⅱ)BC2=BE×CD.
解:(Ⅰ)因为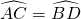 ,
,
所以∠BCD=∠ABC.
又因为EC与圆相切于点C,
故∠ACE=∠ABC
所以∠ACE=∠BCD.(5分)
(Ⅱ)因为∠ECB=∠CDB,∠EBC=∠BCD,
所以△BDC~△ECB,
故 .
.
即BC2=BE×CD.(10分)
分析:(I)先根据题中条件:“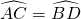 ”,得∠BCD=∠ABC.再根据EC是圆的切线,得到∠ACE=∠ABC,从而即可得出结论.
”,得∠BCD=∠ABC.再根据EC是圆的切线,得到∠ACE=∠ABC,从而即可得出结论.
(II)欲证BC2=BE x CD.即证 .故只须证明△BDC~△ECB即可.
.故只须证明△BDC~△ECB即可.
点评:本题主要考查圆的切线的判定定理的证明、弦切角的应用、三角形相似等基础知识,考查运化归与转化思想.属于基础题.
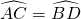 ,
,所以∠BCD=∠ABC.
又因为EC与圆相切于点C,
故∠ACE=∠ABC
所以∠ACE=∠BCD.(5分)
(Ⅱ)因为∠ECB=∠CDB,∠EBC=∠BCD,
所以△BDC~△ECB,
故
 .
.即BC2=BE×CD.(10分)
分析:(I)先根据题中条件:“
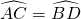 ”,得∠BCD=∠ABC.再根据EC是圆的切线,得到∠ACE=∠ABC,从而即可得出结论.
”,得∠BCD=∠ABC.再根据EC是圆的切线,得到∠ACE=∠ABC,从而即可得出结论.(II)欲证BC2=BE x CD.即证
 .故只须证明△BDC~△ECB即可.
.故只须证明△BDC~△ECB即可.点评:本题主要考查圆的切线的判定定理的证明、弦切角的应用、三角形相似等基础知识,考查运化归与转化思想.属于基础题.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
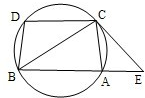 如图:已知圆上的弧
如图:已知圆上的弧
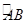 =
=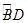 ,过C点的圆的切线与BA的延长线交于E点
,过C点的圆的切线与BA的延长线交于E点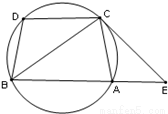
 ,过C点的圆的切线与BA的延长线交于
,过C点的圆的切线与BA的延长线交于  =
= 。
。 =BE x CD。
=BE x CD。 (Ⅰ)
(Ⅰ) E点,证明:
E点,证明: