题目内容
.(本题满分12分)已知焦点在x轴上的双曲线C的两条渐近线经过坐标原点,并且两条渐近线与以点![]() 为圆心、1为半径的圆相切,双曲线C的一个焦点与点A关于直线
为圆心、1为半径的圆相切,双曲线C的一个焦点与点A关于直线![]() 对称. (1)求双曲线C的渐近线和双曲线的方程; (2)设直线
对称. (1)求双曲线C的渐近线和双曲线的方程; (2)设直线![]() 与双曲线C的左支交于P、Q两点,另一直线
与双曲线C的左支交于P、Q两点,另一直线![]() 经过
经过![]() 及线段PQ的中点N,求直线
及线段PQ的中点N,求直线![]() 在
在![]() 轴的截距
轴的截距![]() 的取值范围.
的取值范围.
(1) ![]() (2)
(2) ![]()
解析:
(1) 设双曲线的渐近线方程为![]() ,即
,即![]() ,
,
∵双曲线的渐近线与已知的圆相切,圆心到渐近线的距离等于半径
∴![]()
![]()
![]()
![]()
![]() ∴双曲线的渐近线的方程为:
∴双曲线的渐近线的方程为:![]() ,又设双曲线的方程为:
,又设双曲线的方程为:![]() ,则, ∵双曲线的渐近线的方程为
,则, ∵双曲线的渐近线的方程为![]() ,且有一个焦点为
,且有一个焦点为![]() ∴
∴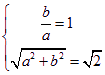
![]() ,
,
解之得:![]() ,故双曲线的方程是:
,故双曲线的方程是:![]()
(2) 联立方程组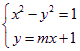 ,消去
,消去![]() 得:
得:![]()
∵直线与双曲线C的左支交于两点,方程(*)两根![]() 、
、![]() 为负数,
为负数,
∴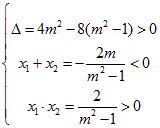
![]()
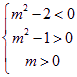
![]()
![]()
又∵线段PQ的中点![]() 坐标满足,
坐标满足,
![]() ,
,![]()
∴直线![]() 的方程为:
的方程为: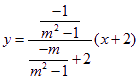 ,即是
,即是![]() ,
,![]() ,直线
,直线![]() 在
在![]() 轴的截距
轴的截距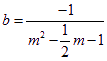
又∵![]() 时,
时,![]() 的取值范围是:
的取值范围是:![]()
∴直线![]() 的截距
的截距![]() 的取值范围是
的取值范围是![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面