题目内容
已知斜率为2的直线l过抛物线y2=px(p>0)的焦点F,且与y轴相交于点A,若△OAF(O为坐标原点)的面积为1,则P=________.

分析:由题意,经过F且斜率为2的直线l方程为y=2(x-
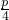 ),与抛物线方程消去y得关于x的一元二次方程,运用根与系数的关系并结合抛物线的定义,可得|AB|=
),与抛物线方程消去y得关于x的一元二次方程,运用根与系数的关系并结合抛物线的定义,可得|AB|= p.用点到直线的距离公式算出原点O到直线AB的距离d=
p.用点到直线的距离公式算出原点O到直线AB的距离d=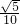 p,根据△OAF面积为1列式,解之可得实数p的值.
p,根据△OAF面积为1列式,解之可得实数p的值.解答:∵抛物线y2=px(p>0)的焦点为F(
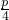 ,0),
,0),∴经过F且斜率为2的直线l方程为y=2(x-
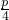 )
)由
 ,消去y得4x2-3px+p2=0
,消去y得4x2-3px+p2=0设A(x1,y1),B(x2,y2),得x1+x2=
 p
p结合抛物线的定义,得|AB|=x1+x2+
 =
= p
p将直线y=2(x-
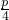 )化成一般式,得2x-y-
)化成一般式,得2x-y- =0
=0∴原点O到直线AB的距离d=
 =
=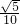 p
p由此可得,△OAF的面积为S△OAF=
 ×|AB|×d=1,即
×|AB|×d=1,即 ×
× p×
p×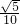 p=1
p=1解之得p=

故答案为:

点评:本题给出抛物线的焦点弦与原点构成面积为1的三角形,求参数p之值,着重考查了抛物线的方程、简单几何性质和直线与抛物线的关系等知识,属于中档题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
已知斜率为2的直线l过抛物线y2=ax的焦点F,且与y轴相交于点A,若△OAF(O为坐标原点)的面积为4,则抛物线方程为( )
| A、y2=4x | B、y2=8x | C、y2=4x或y2=-4x | D、y2=8x或y2=-8x |