题目内容
已知l1:ax-2y+1=0,l2:3x+(1-b)y+1=0,a>0,b>0,若l1⊥l2,则
+
的最小值是( )
| 1 |
| a |
| 2 |
| b |
分析:根据l1⊥l2的充要条件求出a与b的关系,再利用基本不等式,进而得到答案.
解答:解:∵l1:ax-2y+1=0,l2:3x+(1-b)y+1=0,l1⊥l2,
∴3a-2(1-b)=0
∴3a+2b=2
∴
a+b=1
∵a>0,b>0
∴
+
=(
+
)(
a+b)=
+
+
≥
+2
∴
+
的最小值是
+2
故选D.
∴3a-2(1-b)=0
∴3a+2b=2
∴
| 3 |
| 2 |
∵a>0,b>0
∴
| 1 |
| a |
| 2 |
| b |
| 1 |
| a |
| 2 |
| b |
| 3 |
| 2 |
| 7 |
| 2 |
| b |
| a |
| 3a |
| b |
| 7 |
| 2 |
| 3 |
∴
| 1 |
| a |
| 2 |
| b |
| 7 |
| 2 |
| 3 |
故选D.
点评:本题主要考查线线垂直的充要条件,考查基本不等式的运用,解题的关键是利用“1”的代换,进而利用基本不等式.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
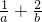 的最小值是
的最小值是



 的最小值是( )
的最小值是( )



 的最小值是( )
的最小值是( )


