题目内容
设p,q为实数,α,β是方程x2-px+q=0的两个实根.数列{xn}满足x1=p,x2=p2-q,xn=pxn-1-qxn-2(n=3,4,…).(1)证明α+β=p,αβ=q;
(2)求数列{xn}的通项公式;
(3)若p=1,q=![]() ,求{xn}的前n项和Sn.
,求{xn}的前n项和Sn.
解:(1)由于α,β为方程x2-px+q=0的根,
则(x-α)(x-β)=x2-px+q![]() α+β=p,αβ=q.
α+β=p,αβ=q.
(2)由α+β=p,αβ=q.
从而设xn=pxn-1-qxn-2)可写成xn=(α+β)xn-1-αβxn-2(n=3,4,…).
∴xn-αxn-1=β(xn-1-αxn-2)(n=3,4,…).
令yn=xn-αxn-1(n=2,3,…),
则有y2=x2-αx1=p2-p+αp=β2,
yn=βyn-1=β2yn-2=…=βn-2y2=βn(n≥3).
故当n≥3时,xn=αxn-1+yn=αxn-1+βn
=α(αxn-2+βn-1)+βn=α2xn-2+(αβn-1+βn)
=……
=αn-2x2+(αn-3β3+αn-4β4+…αβn-1+βn).
而x1=α+β,x2=(α+β)2-αβ=α2+αβ+β2,
所以当n≥3时xn=αn+αn-1β+αn-2β2+…+αβn-1+βn.
故对n≥1都有xn=αn+αn-1β+αn-2β2+…+αβn-1+βn.
故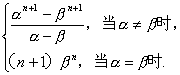
(3)把p=1,q=![]() ,则α=β=
,则α=β=![]() ,这时xn=(n+1)βn=
,这时xn=(n+1)βn=![]() .
.
其前n项和为
Sn=2β1+3β2+…+(n+1)βn=1β0+2β1+3β2+…+(n+1)βn-1β0,
且Sn-βSn=β0+β1+β2+…+βn-(n+1)βn+1-β0(1-β)
=![]()
∵β=![]()
![]() 1-β=
1-β=![]() ,
,
故Sn=2[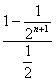 -(n+1)
-(n+1)![]() -
-![]() ]=3-
]=3-![]() .
.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
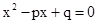 的两个实根,数列
的两个实根,数列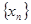 满足
满足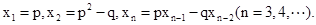

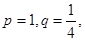 求
求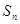 。
。