题目内容
10.已知等差数列{an}中,a1=1,a7=-11,(1)求数列{an}的通项公式;
(2)若数列{an}的前k项和Sk=-80,求k的值.
分析 (1)利用等差数列的通项公式即可得出.
(2)利用等差数列的求和公式即可得出.
解答 解:(1)设等差数列{an}的公差为d,∵a1=1,a7=-11,∴-11=1+6d,解得d=-2.
∴an=1-2(n-1)=3-2n.
(2)Sk=-80=$\frac{k(1+3-2k)}{2}$,化为:k2-2k-80=0,k∈N*,解得k=10.
点评 本题考查了等差数列通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
18.下列函数中,既不是奇函数,也不是偶函数的是( )
| A. | y=x+sin 2x | B. | y=x2-cos x | C. | y=2x+$\frac{1}{{2}^{x}}$ | D. | y=x2+sin x |
16.已知函数y=f(x)是函数y=3x的反函数,则$f({\frac{1}{9}})$=( )
| A. | -2 | B. | 2 | C. | 3 | D. | -3 |
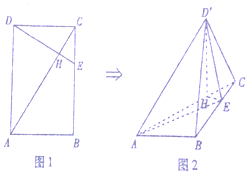 如图1,已知矩形ABCD中,点E是边BC上的点,DE与AC相交于点H,且CE=1,AB=$\sqrt{3}$,BC=3,现将△ACD沿AC折起,如图2,点D的位置记为D′,此时ED′=$\frac{\sqrt{10}}{2}$
如图1,已知矩形ABCD中,点E是边BC上的点,DE与AC相交于点H,且CE=1,AB=$\sqrt{3}$,BC=3,现将△ACD沿AC折起,如图2,点D的位置记为D′,此时ED′=$\frac{\sqrt{10}}{2}$