题目内容
【题目】若函数![]() 的反函数记为
的反函数记为![]() ,已知函数
,已知函数![]() .
.
(1)设函数![]() ,试判断函数
,试判断函数![]() 的极值点个数;
的极值点个数;
(2)当![]() 时,
时,![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 个;(2)
个;(2)![]() .
.
【解析】
试题分析:(1)对函数![]() 求导,判断单调性,根据零点存在性定理得出极值点个数;(2)构造新函数
求导,判断单调性,根据零点存在性定理得出极值点个数;(2)构造新函数![]() ,求导判断导函数的正负情况,先研究不带参数的部分,
,求导判断导函数的正负情况,先研究不带参数的部分,![]() 得到
得到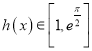 ,因此把
,因此把![]() 分为三部分,研究
分为三部分,研究![]() ,
,![]() 和
和![]() 得出函数
得出函数![]() 的单调性和最值,从而求出
的单调性和最值,从而求出![]() 的范围.
的范围.
试题解析:(1)![]() ,当
,当![]() 时,
时,![]() 是减函数,
是减函数,![]() 也是减函数,
也是减函数,
∴![]() 在
在![]() 上是减函数,当
上是减函数,当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上有且只有一个变号零点,
上有且只有一个变号零点,
∴![]() 在定义域
在定义域![]() 上有且只有一个极值点..
上有且只有一个极值点..
(2)令![]() ,要使
,要使![]() 总成立,只需
总成立,只需![]() 时,
时,![]() ,对
,对![]() 求导得
求导得![]() ,
,
令![]() ,则
,则![]() ,
,![]()
∴![]() 在
在![]() 上为增函数,∴
上为增函数,∴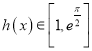 .
.
①当![]() 时,
时,![]() 恒成立,∴
恒成立,∴![]() 在
在![]() 上为增函数,∴
上为增函数,∴![]() ,即
,即
![]() 恒成立;
恒成立;
②当![]() 时,
时,![]() 在上有实根
在上有实根![]() ,∵
,∵![]() 在
在![]() 上为增函数,
上为增函数,
∴当![]() 时,
时,![]() ,∴
,∴![]() ,不符合题意;
,不符合题意;
③当![]() 时,
时,![]() 恒成立,∴
恒成立,∴![]() 在
在![]() 上为减函数,则
上为减函数,则![]() ,不符合题意.
,不符合题意.
综合①②③可得,所求的实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目