题目内容
在△ABC中,已知tan①tanA·cotB=1 ②0<sinA+sinB≤![]() ③sin2A+cos2B=1 ④cos2A+cos2B=sin2C
③sin2A+cos2B=1 ④cos2A+cos2B=sin2C
A.①③ B.②④ C.①④ D.②③
解析:∵tan![]() =tan
=tan![]() =tan(90°-
=tan(90°-![]() )=cot
)=cot![]() =
=![]() =sinC=2sin
=sinC=2sin![]() cos
cos![]() ,
,
∴1=2sin2![]() .∴1-2sin2
.∴1-2sin2![]() =cosC=0.
=cosC=0.
∴C=90°.∴A+B=90°.
∴tanA·cotB=tanA·cot(90°-A)=tanA·tanA=tan2A=1不一定成立,
∴①错误.
∵sin2A+cos2B=sin2A+cos2(90°-B)=sin2A+sin2B=1不一定成立,
∴③错.
∵0<sinA+sinB=sinA+sin(90°-A)=sinA+cosA=![]() sin(A+45°)≤
sin(A+45°)≤![]() ,
,
∴②正确.
∵cos2A+cos2B=cos2A+cos2(90°-A)=cos2A+sin2A=1=sin2C.
∴④正确.故选择B.
答案:B

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 )
) ,H是△ABC的垂心,且
,H是△ABC的垂心,且 .
. 的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,求当△CPQ为锐角三角形时t的取值范围.
的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,求当△CPQ为锐角三角形时t的取值范围.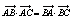 .
. |=|
|=| |;
|; ,求|
,求| -t
-t