题目内容
已知函数f(x)=x+ +b(x≠0),其中a、b为实常数.
+b(x≠0),其中a、b为实常数.
(1)若方程f(x)=3x+1有且仅有一个实数解x=2,求a、b的值;
(2)设a>0,x∈(0,+∞),写出f(x)的单调区间,并对单调递增区间用函数单调性定义进行证明;
(3)若对任意的a∈[ ,2],不等式f(x)≤10在x∈[
,2],不等式f(x)≤10在x∈[ ,1]上恒成立,求实数b的取值范围.
,1]上恒成立,求实数b的取值范围.
解:(1)由已知,方程)=x+ +b=3x+1有且仅有一个解x=2,
+b=3x+1有且仅有一个解x=2,
因为x≠0,故原方程可化为2x2+(1-b)x-a=0,
所以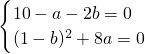 ,…解得a=-8,b=9.
,…解得a=-8,b=9.
(2)当a>0,x>0时,f(x)在区间(0, )上是减函数,在(
)上是减函数,在( ,+∞)上是增函数.
,+∞)上是增函数.
证明:设x1,x2∈( ,+∞),且x1<x2,
,+∞),且x1<x2,
f(x2)-f(x1)=x2+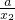 -x1-
-x1-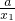 =(x2-x1)•
=(x2-x1)•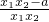 ,
,
因为x1,x2∈( ,+∞),且x1<x2,
,+∞),且x1<x2,
所以x2-x1>0,x1x2>a,
所以f(x2)-f(x1)>0.
所以f(x)在( ,+∞)上是增函数.
,+∞)上是增函数.
(3)因为f(x)≤10,故x∈[ ,1]时有f(x)max≤10,
,1]时有f(x)max≤10,
由(2),知f(x)在区间[ ,1]的最大值为f(
,1]的最大值为f( )与f(1)中的较大者.
)与f(1)中的较大者.
所以,对于任意的a∈[ ,2],不等式f(x)≤10在x∈[
,2],不等式f(x)≤10在x∈[ ,1]上恒成立,当且仅当
,1]上恒成立,当且仅当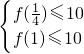 ,
,
即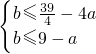 对任意的a∈[
对任意的a∈[ ,2]成立.
,2]成立.
从而得到b≤ .
.
所以满足条件的b的取值范围是(-∞, ].
].
分析:(1)依题意,原方程可化为2x2+(1-b)x-a=0,由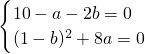 即可解得a、b的值;
即可解得a、b的值;
(2)当a>0,x>0时,f(x)在区间(0, )上是减函数,在(
)上是减函数,在( ,+∞)上是增函数;利用定义证明时,先设x1,x2∈(
,+∞)上是增函数;利用定义证明时,先设x1,x2∈( ,+∞),且x1<x2,再作差f(x2)-f(x1)后化积讨论即可;
,+∞),且x1<x2,再作差f(x2)-f(x1)后化积讨论即可;
(3)依题意得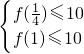 ,可解得到b≤
,可解得到b≤ ,从而可得实数b的取值范围.
,从而可得实数b的取值范围.
点评:本题考查函数恒成立问题,考查函数单调性的判断与证明,考查方程思想与等价转化思想的综合运用,属于难题.
 +b=3x+1有且仅有一个解x=2,
+b=3x+1有且仅有一个解x=2,因为x≠0,故原方程可化为2x2+(1-b)x-a=0,
所以
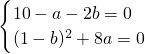 ,…解得a=-8,b=9.
,…解得a=-8,b=9.(2)当a>0,x>0时,f(x)在区间(0,
 )上是减函数,在(
)上是减函数,在( ,+∞)上是增函数.
,+∞)上是增函数.证明:设x1,x2∈(
 ,+∞),且x1<x2,
,+∞),且x1<x2,f(x2)-f(x1)=x2+
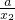 -x1-
-x1-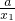 =(x2-x1)•
=(x2-x1)•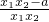 ,
,因为x1,x2∈(
 ,+∞),且x1<x2,
,+∞),且x1<x2,所以x2-x1>0,x1x2>a,
所以f(x2)-f(x1)>0.
所以f(x)在(
 ,+∞)上是增函数.
,+∞)上是增函数.(3)因为f(x)≤10,故x∈[
 ,1]时有f(x)max≤10,
,1]时有f(x)max≤10,由(2),知f(x)在区间[
 ,1]的最大值为f(
,1]的最大值为f( )与f(1)中的较大者.
)与f(1)中的较大者.所以,对于任意的a∈[
 ,2],不等式f(x)≤10在x∈[
,2],不等式f(x)≤10在x∈[ ,1]上恒成立,当且仅当
,1]上恒成立,当且仅当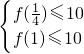 ,
,即
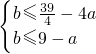 对任意的a∈[
对任意的a∈[ ,2]成立.
,2]成立.从而得到b≤
 .
. 所以满足条件的b的取值范围是(-∞,
 ].
]. 分析:(1)依题意,原方程可化为2x2+(1-b)x-a=0,由
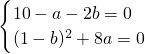 即可解得a、b的值;
即可解得a、b的值;(2)当a>0,x>0时,f(x)在区间(0,
 )上是减函数,在(
)上是减函数,在( ,+∞)上是增函数;利用定义证明时,先设x1,x2∈(
,+∞)上是增函数;利用定义证明时,先设x1,x2∈( ,+∞),且x1<x2,再作差f(x2)-f(x1)后化积讨论即可;
,+∞),且x1<x2,再作差f(x2)-f(x1)后化积讨论即可;(3)依题意得
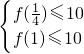 ,可解得到b≤
,可解得到b≤ ,从而可得实数b的取值范围.
,从而可得实数b的取值范围.点评:本题考查函数恒成立问题,考查函数单调性的判断与证明,考查方程思想与等价转化思想的综合运用,属于难题.

练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|