题目内容
若△ABC的内角A、B、C所对的边a、b、c满足 ,且
,且 =60°,则
=60°,则  的值为( )
的值为( )
A. B.1 C.
B.1 C. D.
D.
C
解析试题分析:由 得:
得: ,故由余弦定理知:
,故由余弦定理知:
 ,解得
,解得 ,故选C.
,故选C.
考点:余弦定理的应用

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
在 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,且
,且 则角
则角 的大小为( )
的大小为( )
A. | B. | C. | D. |
在 中,
中,  ,
, ,则
,则 的最小值是( )
的最小值是( )
A. | B. | C. | D. |
 的三个内角
的三个内角 所对的边分别为
所对的边分别为 ,给出下列三个叙述:
,给出下列三个叙述:
①
②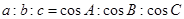
③
以上三个叙述中能作为“ 是等边三角形”的充分必要条件的个数为( )
是等边三角形”的充分必要条件的个数为( )
| A.0个 | B.1个 | C.2个 | D.3个 |
在△ABC中,若a = 2 , ,
, , 则B等于( )
, 则B等于( )
A. | B. 或 或  | C. | D. 或 或 |
在△ 中,角
中,角 的对边为
的对边为 ,若
,若 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
在△ABC中,角A,B,C所对的边长分别为a,b,c,若∠C=120°,c= a,则( ).
a,则( ).
| A.a>b | B.a<b |
| C.a=b | D.a与b的大小关系不能确定 |
若 的内角
的内角 所对的边
所对的边 满足
满足 ,且
,且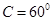 ,则
,则  的值为( )
的值为( )
A. | B. 1 1 | C. | D. |
 ] B.(0,
] B.(0, ]
]