题目内容
 的三个内角
的三个内角 所对的边分别为
所对的边分别为 ,给出下列三个叙述:
,给出下列三个叙述:
①
②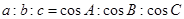
③
以上三个叙述中能作为“ 是等边三角形”的充分必要条件的个数为( )
是等边三角形”的充分必要条件的个数为( )
| A.0个 | B.1个 | C.2个 | D.3个 |
C
解析试题分析:根据正弦定理,无论是何三角形都有① ,即不能作为“
,即不能作为“ 是等边三角形”的充分必要条件;而由正弦定理
是等边三角形”的充分必要条件;而由正弦定理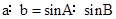 ,且
,且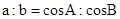 ,
,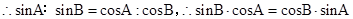 ,所以, sin(B-A)=0,因而,
,所以, sin(B-A)=0,因而,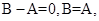 同理可得
同理可得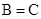 ,得三角形ABC是等边三角形. ②
,得三角形ABC是等边三角形. ②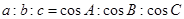 能作为“
能作为“ 是等边三角形”的充分必要条件;
是等边三角形”的充分必要条件;
由正弦定理 及条件
及条件 ,得,
,得,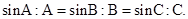
构造函数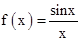 ,
,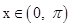 则
则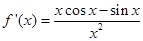 ,
,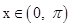 时,总有
时,总有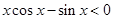 , 故
, 故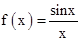 在
在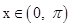 是单调减函数,所以,A="B=C" , 从而三角形是正三角形,即③
是单调减函数,所以,A="B=C" , 从而三角形是正三角形,即③ 能作为“
能作为“ 是等边三角形”的充分必要条件.故选C.
是等边三角形”的充分必要条件.故选C.
考点:正弦定理的应用,充要条件,应用导数研究函数的单调性.

练习册系列答案
相关题目
在 中,
中, ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
在△ABC中, 所对的边分别为
所对的边分别为 ,若ccosC=bcosB,则△ABC的形状一定是( )
,若ccosC=bcosB,则△ABC的形状一定是( )
| A.等腰三角形 | B.直角三角形 | C.等腰或直角三角形 | D.等边三角形 |
已知 中,内角
中,内角 所对边长分别为
所对边长分别为 ,若
,若 ,则
,则 的面积等于( )
的面积等于( )
A. | B. | C. | D. |
在 中角
中角 、
、 、
、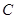 的对边分别是
的对边分别是 、
、 、
、 ,若
,若 ,则
,则 为( )
为( )
A. | B. | C. | D. |
 中,三边长
中,三边长 满足
满足 ,那么
,那么 的形状为( )
的形状为( )
| A.锐角三角形 | B.钝角三角形 | C.直角三角形 | D.以上均有可能 |
在△ABC中,若∠A∶∠B∶∠C=1∶2∶3,则a∶b∶c等于
| A.1∶2∶3 | B.3∶2∶1 | C. | D. |
 (
( >
> )的焦点为
)的焦点为 ,已知点
,已知点 、
、 为抛物线上的两个动点,且满足
为抛物线上的两个动点,且满足 .过弦
.过弦 的中点
的中点 作抛物线准线的垂线
作抛物线准线的垂线 ,垂足为
,垂足为 ,则
,则 的最大值为 ( )
的最大值为 ( )

 ,且
,且 =60°,则
=60°,则  的值为( )
的值为( ) B.1 C.
B.1 C. D.
D.