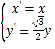Question

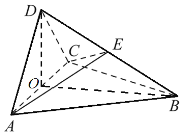
【题目】已知空间9点集，其中任意四点不共面.在这9个点间联结若干条线段，构成一个图G，使图中不存在四面体.问图G中最多有多少个三角形？

Answer 1

【答案】27

【解析】

在一个n个点的空间图中不存在三角形，则其边数不超过.

证明:设这n个点为，其中从引出的边数最多，不妨设共有k条:.依条件，不存在三角形，那么，点之间没有边相连.从而，空间图中每条边均至少有一个端点为中的点而每个至多引出k条边.因此，总边数小于或等于k

下面证明空间9点集M中，若任意4点不共面，在这9点间联结若干条线段，如果图G中已有（至少）28个三角形，则至少有一个四面体.

用反证法.

假设不存在一个四面体，在9点集中，由抽屉原理知，其中必有一点为至少个三角形的顶点.从而，由这个点至少引出5条边，设这个点为

(1).若从点引出5条边，依题意，由于没有四面体，那么，由这5个点构成的子图中没有三角形.由前面的结论知，这个子图中至多有条边.从而.以为顶点的三角形至多有6个，矛盾.

（2）若从点引出6条边，类似(1)，至多有个三角形以为顶点,矛盾.

（3）若从点引出7条边，由于没有四面体，可知这7个点构成的子图中没有三角形,这个子图至多有条边.从而，以为顶点的三角形至多有12个，不以为顶点的三角形必以点为一个顶点.类似地也至多有12个三角形，那么，三角形总数小于或等于12×2-24<28，矛盾.

（4）若从点引出8条边，这时,，A这8个点构成的子图中没有三角形.由前面的结论知，至多有条边.从而，原图G中至多有16个三角形,矛盾.

于是，满足要求的三角形至多有27个.

将9点集M分成三组，，，使同组中任两点不连线，而不同组中的两点均连线，这样有个三角形,当然没有四面体.