题目内容
已知M、N分别是正方体ABCD—A1B1C1D1的棱B1C1和B1B的中点.(1)求MN与A1C1所成角的大小;
(2)求MN与平面ACC1A1所成角的大小.
解析:方法一:如图甲,(1)连结BC1、A1B.
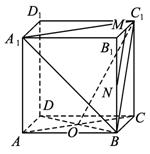
甲
∵M、N分别是B1C1、B1B的中点,
∴MN∥BC1.
∴∠A1C1B是MN与A1C1所成的角(或其补角).
而△A1BC1为等边三角形,
∴∠A1C1B=60°.
∴MN与A1C1成60°角.
(2)由(1)可知MN∥BC1,
∴MN与平面A1C所成角等于BC1与平面A1C所成角.
连结BD,AC∩BD=O,易证BO⊥平面A1C.
∴∠BC1O为BC1与平面A1C所成角.
设正方体棱长为a,则BO=![]() a,BC1=
a,BC1=![]() a.
a.
∴∠BC1O=30°.
∴MN与平面AC1所成角为30°.
方法二:(1)设正方体的棱长为1,建立直角坐标系D—xyz(如图乙).

乙
则A1(1,0,1),C1(0,1,1),M(![]() ,1,1),N(1,1,
,1,1),N(1,1,![]() ).∴
).∴![]() =(
=(![]() ,0,-
,0,-![]() ),
),![]() =(-1,1,0).
=(-1,1,0).
∴cos〈![]() ,
,![]() 〉
〉
=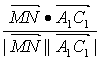 =
=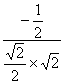 =-
=-![]() .
.
∴〈![]() ,
,![]() 〉=120°.
〉=120°.
而异面直线所成角在(0,90°]内,
∴MN与A1C1成60°角.
(2)设平面A1C的法向量n=(1,α,β),则n⊥![]() ,(1,α,β)·(0,0,1)=0,
,(1,α,β)·(0,0,1)=0,
∴β=0.
又n⊥![]() .
.
∴(1,α,β)·(-1,1,0)=0.
∴a=1.
∴n=(1,1,0).
∴cos〈n, ![]() 〉=
〉= =
=![]() .
.
∴〈n, ![]() 〉=60°.
〉=60°.
∴MN与面AC1成30°角.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标.
如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标.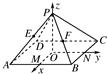 如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标.
如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标.