题目内容
已知数列{an}、{bn}满足: .
.
(1)求b1,b2,b3,b4;
(2)求数列{bn}的通项公式;
(3)设Sn=a1a2+a2a3+a3a4+…+anan+1,求实数a为何值时4aSn<bn恒成立.
解:(1)∵
∴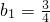 ,
, ,
,
 ,
, ,
,
(2)∵
∴
∴数列{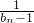 }是以-4为首项,-1为公差的等差数列
}是以-4为首项,-1为公差的等差数列
∴
∴ ;
;
(3) ,
,
∴
∴
由条件可知(a-1)n2+(3a-6)n-8<0恒成立即可满足条件,
设f(n)=(a-1)n2+(3a-6)n-8
当a=1时,f(n)=-3n-8<0恒成立
当a>1时,由二次函数的性质知不可能成立
当a<1时,对称轴
f(n)在(1,+∞)为单调递减函数.
f(1)=(a-1)n2+(3a-6)n-8=(a-1)+(3a-6)-8=4a-15<0
∴ ∴a<1时4aSn<b恒成立
∴a<1时4aSn<b恒成立
综上知:a≤1时,4aSn<b恒成立.
分析:(1)根据 ,求出
,求出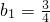 ,和
,和 ,令n=1,2,3即可求得b1,b2,b3,b4;
,令n=1,2,3即可求得b1,b2,b3,b4;
(2)根据 ,进行变形得到
,进行变形得到 ,构造等差数列{
,构造等差数列{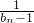 },并求出其通项,进而可求出数列{bn}的通项公式;
},并求出其通项,进而可求出数列{bn}的通项公式;
(3)根据(2)结果,可以求出数列{an}的通项公式,然后利用裂项相消法求Sn,构造函数f(n)=(a-1)n2+(3a-6)n-8,转化为求函数f(n)的最值问题,可求实数a的取值范围.
点评:此题是个难题.考查根据数列的递推公式利用构造法求数列的通项公式,及数列的求和问题,题目综合性强,特别是问题(3)的设置,数列与不等式恒成立问题结合起来,能有效考查学生的逻辑思维能力,体现了转化的思想和分类讨论的思想.

∴
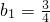 ,
, ,
, ,
, ,
,
(2)∵

∴

∴数列{
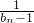 }是以-4为首项,-1为公差的等差数列
}是以-4为首项,-1为公差的等差数列∴

∴
 ;
;(3)
 ,
,∴

∴

由条件可知(a-1)n2+(3a-6)n-8<0恒成立即可满足条件,
设f(n)=(a-1)n2+(3a-6)n-8
当a=1时,f(n)=-3n-8<0恒成立
当a>1时,由二次函数的性质知不可能成立
当a<1时,对称轴

f(n)在(1,+∞)为单调递减函数.
f(1)=(a-1)n2+(3a-6)n-8=(a-1)+(3a-6)-8=4a-15<0
∴
 ∴a<1时4aSn<b恒成立
∴a<1时4aSn<b恒成立综上知:a≤1时,4aSn<b恒成立.
分析:(1)根据
 ,求出
,求出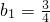 ,和
,和 ,令n=1,2,3即可求得b1,b2,b3,b4;
,令n=1,2,3即可求得b1,b2,b3,b4;(2)根据
 ,进行变形得到
,进行变形得到 ,构造等差数列{
,构造等差数列{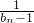 },并求出其通项,进而可求出数列{bn}的通项公式;
},并求出其通项,进而可求出数列{bn}的通项公式;(3)根据(2)结果,可以求出数列{an}的通项公式,然后利用裂项相消法求Sn,构造函数f(n)=(a-1)n2+(3a-6)n-8,转化为求函数f(n)的最值问题,可求实数a的取值范围.
点评:此题是个难题.考查根据数列的递推公式利用构造法求数列的通项公式,及数列的求和问题,题目综合性强,特别是问题(3)的设置,数列与不等式恒成立问题结合起来,能有效考查学生的逻辑思维能力,体现了转化的思想和分类讨论的思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目