题目内容
4、(1)证明|sin2x|≤2|sinx|;(x为任意值)
(2)已知n为任意正整数,用数学归纳法证明|sinnx|≤n|sinx|.(x为任意值)
(2)已知n为任意正整数,用数学归纳法证明|sinnx|≤n|sinx|.(x为任意值)
分析:(1)先利用三角函数的二倍角公式,再结合三角函数的有界性即可证明;
(2)用数学归纳法证明三角问题时分为两个步骤,第一步,先证明当当n=1时,结论显然成立,第二步,先假设假设当n=k时结论成立,利用此假设结合三角函数的和角公式以及三角函数值的有界性,证明当n=k+1时,结论也成立即可.
(2)用数学归纳法证明三角问题时分为两个步骤,第一步,先证明当当n=1时,结论显然成立,第二步,先假设假设当n=k时结论成立,利用此假设结合三角函数的和角公式以及三角函数值的有界性,证明当n=k+1时,结论也成立即可.
解答:证:(1)|sin2x|=|2sinx•cosx|=2|sinx|•|cosx|.
∵|cosx|≤1,
∴|sin2x|≤2|sinx|;
(2)当n=1时,结论显然成立.
假设当n=k时结论成立,
即|sinkx|≤k|sinx|.
当n=k+1时,
|sin(k+1)x|
=|sinkx•cosx+coskx•sinx|≤|sinkx•cosx|+|coskx•sinx|
=|sinkx|•|cosx|+|coskx|•|sinx|≤k|sinx|+|sinx|
=(k+1)|sinx|.
故当n为任意正整数时,结论均成立.
∵|cosx|≤1,
∴|sin2x|≤2|sinx|;
(2)当n=1时,结论显然成立.
假设当n=k时结论成立,
即|sinkx|≤k|sinx|.
当n=k+1时,
|sin(k+1)x|
=|sinkx•cosx+coskx•sinx|≤|sinkx•cosx|+|coskx•sinx|
=|sinkx|•|cosx|+|coskx|•|sinx|≤k|sinx|+|sinx|
=(k+1)|sinx|.
故当n为任意正整数时,结论均成立.
点评:本题主要考查数学归纳法,数学归纳法的基本形式
设P(n)是关于自然数n的命题,若1°P(n0)成立(奠基)
2°假设P(k)成立(k≥n0),可以推出P(k+1)成立(归纳),则P(n)对一切大于等于n0的自然数n都成立
设P(n)是关于自然数n的命题,若1°P(n0)成立(奠基)
2°假设P(k)成立(k≥n0),可以推出P(k+1)成立(归纳),则P(n)对一切大于等于n0的自然数n都成立

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
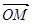 ·
·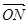 =0,其中点
=0,其中点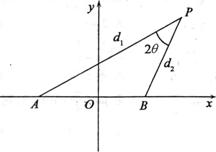
 ;
; .
.