题目内容
设α,β,γ 都是锐角,且sinα+sinβ+sinγ=1,证明(1)sin2α+sin2β+sin2γ≥
 ;
;(2)tan2α+tan2β+tan2 γ≥
 .
.
【答案】分析:(1)根据柯西不等式得:(sin2α+sin2β+sin2γ)(1+1+1)≥(1•sinα+1•sinβ+1•sinγ)2,结合题中条件即可证得;
(2)由恒等式tan2x= 和重要结论:“若a,b,c>0,则
和重要结论:“若a,b,c>0,则 ≥
≥ ,”即可得出:得tan2α+tan2β+tan2 γ=
,”即可得出:得tan2α+tan2β+tan2 γ= +
+ +
+ -3≥
-3≥ -3,再进行放缩即得.
-3,再进行放缩即得.
解答:证明:(1)由柯西不等式得:(sin2α+sin2β+sin2γ)(1+1+1)≥(1•sinα+1•sinβ+1•sinγ)2,
因为sinα+sinβ+sinγ=1,所以3(sin2α+sin2β+sin2γ)≥1,得:sin2α+sin2β+sin2γ≥ .
.
(2)由恒等式tan2x= 和若a,b,c>0,则
和若a,b,c>0,则 ≥
≥ ,
,
得tan2α+tan2β+tan2 γ= +
+ +
+ -3≥
-3≥ -3.
-3.
于是 =
= ≥
≥ =
= ,
,
由此得tan2α+tan2β+tan2 γ≥ -3=
-3= .
.
点评:本小题主要考查一般形式的柯西不等式、三角函数的同角三角函数关系式、不等式的证明等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.
(2)由恒等式tan2x=
 和重要结论:“若a,b,c>0,则
和重要结论:“若a,b,c>0,则 ≥
≥ ,”即可得出:得tan2α+tan2β+tan2 γ=
,”即可得出:得tan2α+tan2β+tan2 γ= +
+ +
+ -3≥
-3≥ -3,再进行放缩即得.
-3,再进行放缩即得.解答:证明:(1)由柯西不等式得:(sin2α+sin2β+sin2γ)(1+1+1)≥(1•sinα+1•sinβ+1•sinγ)2,
因为sinα+sinβ+sinγ=1,所以3(sin2α+sin2β+sin2γ)≥1,得:sin2α+sin2β+sin2γ≥
 .
.(2)由恒等式tan2x=
 和若a,b,c>0,则
和若a,b,c>0,则 ≥
≥ ,
,得tan2α+tan2β+tan2 γ=
 +
+ +
+ -3≥
-3≥ -3.
-3.于是
 =
= ≥
≥ =
= ,
,由此得tan2α+tan2β+tan2 γ≥
 -3=
-3= .
.点评:本小题主要考查一般形式的柯西不等式、三角函数的同角三角函数关系式、不等式的证明等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.

练习册系列答案
相关题目
 (2013•泉州模拟)如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD.
(2013•泉州模拟)如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD.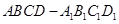 中,
中,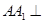 平面
平面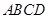 .
.
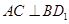 的充分条件,并给予证明;
的充分条件,并给予证明;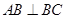 ,②
,②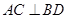 ;③
;③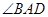 为锐角,求平面
为锐角,求平面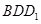 与平面
与平面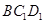 所成锐二面角
所成锐二面角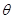 的取值范围.
的取值范围.