题目内容
如图求证:EF＜
(AD+BC).
图
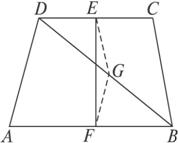
证明:过E作EG∥BC交BD于G,连结GF.
∵DE=EC,EG∥BC,
∴DG=BG.∴EG=
BC.
∵F为AB中点,
∴GF=AD.
∵EF＜EG+GF,∴EF＜
(AD+BC).
练习册系列答案
阅读快车系列答案
相关题目
阅读快车系列答案题目内容
如图求证:EF＜(AD+BC).
图
证明:过E作EG∥BC交BD于G,连结GF.
∵DE=EC,EG∥BC,
∴DG=BG.∴EG=BC.
∵F为AB中点,
∴GF=AD.
∵EF＜EG+GF,∴EF＜(AD+BC).
阅读快车系列答案
上任取一点C(点C与A、B不重合),过点C作半圆的切线CD交AP于点D;过点C作CE⊥AB,垂足为E,连结BD,交CE于点F.
的中点时(如图13(1)),求证:CF =EF;
的中点时(如图13(2)),试判断CF与EF的相等关系是否保持不变,并证明你的结论.
