题目内容
请考生在下列两题中任选一题作答,如果多做,则按所做的第一题记分.(1)极坐标系中,曲线ρ=10cosθ和直线3ρcosθ-4ρsinθ-30=0交于A、B两点,则线段AB的长= .
(2)已知函数f(x)=|x-2|-|x-5|,则f(x)的取值范围是 .
【答案】分析:(1)把曲线的极坐标化为直角坐标,表示一个圆,求出圆心和半径,再求出圆心到直线的距离d,由弦长公式求得 AB=2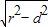 的值.
的值.
(2)根据绝对值的意义,求出函数的最大值和最小值,从而求得f(x)的取值范围.
解答:解:(1)极坐标系中,曲线ρ=10cosθ 即ρ2=10ρcosθ,即 x2+y2=10x,即 (x-5)2+y2=25,表示以(5,0)为圆心,以r=5为半径的圆.
直线3ρcosθ-4ρsinθ-30=0 即 3x-4y-30=0,圆心到直线的距离d=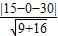 =3,∴AB=2
=3,∴AB=2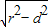 =8,
=8,
故答案为 8.
(2)已知函数f(x)=|x-2|-|x-5|,表示数轴上的x对应点到2对应点的距离减去 它到5对应点的距离,
故函数的最大值为3,最小值为-3,
故函数的值域为[-3,3],
故答案为[-3,3].
点评:本题主要考查把极坐标方程化为直角坐标方程的方法,点到直线的距离公式的应用,直线和圆的位置关系,绝对值的意义,属于基础题.
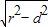 的值.
的值.(2)根据绝对值的意义,求出函数的最大值和最小值,从而求得f(x)的取值范围.
解答:解:(1)极坐标系中,曲线ρ=10cosθ 即ρ2=10ρcosθ,即 x2+y2=10x,即 (x-5)2+y2=25,表示以(5,0)为圆心,以r=5为半径的圆.
直线3ρcosθ-4ρsinθ-30=0 即 3x-4y-30=0,圆心到直线的距离d=
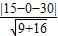 =3,∴AB=2
=3,∴AB=2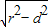 =8,
=8,故答案为 8.
(2)已知函数f(x)=|x-2|-|x-5|,表示数轴上的x对应点到2对应点的距离减去 它到5对应点的距离,
故函数的最大值为3,最小值为-3,
故函数的值域为[-3,3],
故答案为[-3,3].
点评:本题主要考查把极坐标方程化为直角坐标方程的方法,点到直线的距离公式的应用,直线和圆的位置关系,绝对值的意义,属于基础题.

练习册系列答案
相关题目
 选做题:请考生在下列两题中任选一题作答,若两题都做,则按所做的第一题评阅计分.
选做题:请考生在下列两题中任选一题作答,若两题都做,则按所做的第一题评阅计分.