Question

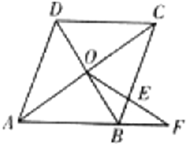
选做题：请考生在下列两题中任选一题作答，若两题都做，则按所做的第一题评阅计分．
（1）（几何证明选讲选做题） 如图，平行四边形ABCD的对角线AC和BD交于点O，OE与BC和AB的延长线分别交于点E和F，若AB=2，BC=3，BF=1，则BE=

3

4

．
（2）（坐标系与参数方程选做题） 若直线l1：

x=1-2t y=2+kt.

(t为参数)，
与直线l2：

x=s y=1-2s.

（s为参数）垂直，则k=

-1

．

Answer 1

分析：（1）本题先延长FO与AD相较于M点，由AD∥BC，即可得比例式：

BE

AM

=

BF

AF

，

BE

DM

=

BO

DO

=1，进而可求的BE的长．
（2）将直线的参数方程化为普通方程，即可得出直线的斜率，利用两直线垂直的条件可得两直线的斜率乘积等于-1，即可求出k的值．

解答：解：（1）如图所示：将FO延长与AD相交于M，设BE=x，∵BE∥AD，∴

BE

AM

=

BF

AF

，

BE

DM

=

BO

DO

=1，
∴DM=x，
又∵AB=2，BF=1，∴

x

AM

=

1

3

，∴AM=3x，∵AD=BC=3，∴x+3x=3，∴x=

3

4

．∴BE=

3

4

．
故答案

3

4

．          
（2）将两直线的参数方程分别化为普通方程：l₁：y-2=

-k

2

（x-1）；  l₂：y-1=-2x，可知直线l₁的斜率k₁=

-k

2

，直线l₂的斜率k₂=-2，
∵l₁⊥l₂，∴k₁×k₂=-1，即

-k

2

×(-2)=-1，解得k=-1．
故答案为-1．

点评：本题一是考查了利用平行线分线段成比例，一是考查给出两垂直的直线参数方程求斜率的乘积为-1，恰当的作出辅助线和准确画参数方程为普通方程是解决问题的关键．