题目内容
如图,α⊥B,α∩B=l,A∈α,B∈B,点A在直线l上的射影为A1,点B在l上的射影为B1.已知AB=2,AA1=1,BB1=(1)直线AB分别与平面α,B所成角的大小;
(2)二面角A1—AB—B1的大小.
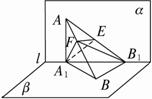
解:(1)如图,连结A1B,AB1.

∵α⊥B,α∩B=l,AA1⊥l,BB1⊥l,
∴AA1⊥B,BB1⊥α,
则∠BAB1,∠ABA1分别是AB与α和B所成的角.Rt△BB![]() ,AB=2.
,AB=2.
∴sinBAB1=![]() ,
,
∴∠BAB1=45°.
Rt△AA1B中,AA1=1,AB=2.
∴sinABA1=![]() .
.
∴∠ABA1=30°.
故AB与平面α,B所成的角分别是45°,30°.
(2)∵BB1⊥α,∴平面ABB1⊥α,在平面α内过A1作A1E⊥AB1交AB1于E,则A1E⊥平面AB1B,过E作EF⊥AB交AB于F,连结A
∴∠A1FE就是所求二面角的平面角.
在Rt△ABB1中,∠BAB1=45°,∴AB1=B1B=![]() .
.
在Rt△AA1B1中,AA1=A1B1=1,∴A1E=![]() AB1=
AB1=![]() .
.
在Rt△AA1B中,A1B=![]() .
.
由AA1·A1B=A![]() ,
,
∴在Rt△A1EF中,sinA1FE=![]() .
.
∴二面角A1—AB—B1的大小为arcsin![]() .
.

练习册系列答案
相关题目
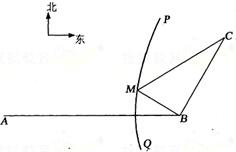 如图,B地在A地的正东方向4km处,C地在B地的北偏东30°方向2km处,河流
如图,B地在A地的正东方向4km处,C地在B地的北偏东30°方向2km处,河流的没岸PQ(曲线)上任意一点到A的距离比到B的距离远2km.现要在曲线PQ上一处M建一座码头,向B、C两地转运货物.经测算,从M到B、M到C修建公路的费用分别是a万元/km、2a万元/km,那么修建这两条公路的总费用最低是( )
A、(2
| ||
| B、5a万元 | ||
C、(2
| ||
D、(2
|
 如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A(x1,y1),B(x2,y2)两点.
如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A(x1,y1),B(x2,y2)两点.
 (选做题)在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
(选做题)在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.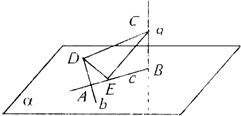 (2007•青岛一模)如图所示,b、c在平面α内,a∩c=B,b∩c=A,且a⊥b,a⊥c,b⊥c,若C∈a,D∈b,E在线段AB上(C,D,E均异于A,B),则△CDE是( )
(2007•青岛一模)如图所示,b、c在平面α内,a∩c=B,b∩c=A,且a⊥b,a⊥c,b⊥c,若C∈a,D∈b,E在线段AB上(C,D,E均异于A,B),则△CDE是( )