题目内容
已知a+b+c=1，m=a2+b2+c2，则m的最小值为________．
分析：对于“积和结构”或“平方和结构”，通常构造利用柯西不等式求解即可．
解答：由柯西不等式得，（a2+b2+c2）（1+1+1）≥（a+b+c）2
当且仅当a=b=c时，取等号
∵a+b+c=1，m=a2+b2+c2，
∴3m≥1
∴m
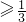
故答案为：
点评：柯西不等式的特点：一边是平方和的积，而另一边为积的和的平方，因此，当欲证不等式的一边视为“积和结构”或“平方和结构”，再结合不等式另一边的结构特点去尝试构造．
练习册系列答案
相关题目
．
．
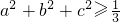