Question

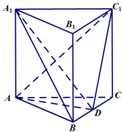（2013•大兴区一模）如图，直三棱柱ABC-A₁B₁C₁中，△ABC是等边三角形，D是BC的中点．
（Ⅰ）求证：A₁B∥平面ADC₁；
（Ⅱ）若AB=BB₁=2，求A₁D与平面AC₁D所成角的正弦值．

Answer 1

分析：（I）连接A₁C交AC₁于E，利用直三棱柱的性质、矩形的性质、三角形中位线的性质定理即可得到ED∥A₁B，再利用线面平行的判定定理即可证明；
（II）建立如图所示空间坐标系D-xyz．利用直线的方向向量和平面的法向量的夹角即可得出线面角．

解答：证明：（I）∵三棱柱ABC-A₁B₁C₁是直三棱柱，∴四边形A₁ACC₁是矩形．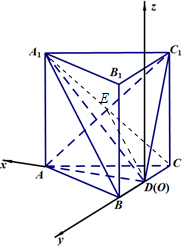
连接A₁C交AC₁于E，则E是A₁C的中点，
又D是BC的中点，在△A₁BC中，ED∥A₁B．
∵A₁B?平面ADC₁，ED?平面ADC₁，∴A₁B∥平面ADC₁．
（II）∵△ABC是等边三角形，D是BC的中点，∴AD⊥BC．
以D为原点，建立如图所示空间坐标系D-xyz．
由已知AB=BB₁=2，得：D（0，0，0），A(

3

，0，0)，A1(

3

，0，2)，C₁（0，-1，2）．
则

DA

=(

3

，0，0)，

DC1

=(0，-1，2)，
设平面ADC₁的法向量为

n

=(x，y，z)．
由

n • DA =0 n • DC1 =0

，得到

3 x=0 -y+2z=0

，令z=1，则x=0，y=2，
∴

n

=(0，2，1)．
又

DA1

=(

3

，0，2)，得

n

•

DA1

=0×

3

+2×0+1×2=2．
∴cos＜

DA1

，

n

＞=

2

5 × 7

=

2 35

35

设A₁D与平面ADC₁所成角为θ，
则sinθ=|cos＜

DA1

，

n

＞|=

2 35

35

．
所以A₁D与平面ADC₁所成角的正弦值为

2 35

35

．

点评：熟练掌握直三棱柱的性质、矩形的性质、三角形中位线的性质定理、线面平行的判定定理、建立空间坐标系利用直线的方向向量和平面的法向量的夹角得出线面角的方法等是解题的关键..