题目内容
设f(x)是R上的偶函数,且在[0,+∞)上单调递增,则f(-2),f(3),f(-π)的大小顺序是( )A.f(-π)>f(3)>f(-2)
B.f(-π)>f(-2)>f(3)
C.f(-2)>f(3)>f(-π)
D.f(3)>f(-2)>f(-π)
【答案】分析:利用函数的单调性比较函数值的大小,需要在同一个单调区间上比较,利用偶函数的性质,f(-2)=f(2),f(-π)=f(π)转化到同一个单调区间上,再借助于单调性求解即可比较出大小.
解答:解:由已知f(x)是R上的偶函数,所以有f(-2)=f(2),f(-π)=f(π),
又由在[0,+∞]上单调增,且2<3<π,所以有
f(2)<f(3)<f(π),
所以f(-2)<f(3)<f(-π),
故答案为:f(-π)>f(3)>(-2).
故选:A.
点评:本题考查函数的奇偶性与函数的单调性,以及它们的综合应用,函数值的大小比较,要利用单调性,统一在某个单调区间上比较大小.
解答:解:由已知f(x)是R上的偶函数,所以有f(-2)=f(2),f(-π)=f(π),
又由在[0,+∞]上单调增,且2<3<π,所以有
f(2)<f(3)<f(π),
所以f(-2)<f(3)<f(-π),
故答案为:f(-π)>f(3)>(-2).
故选:A.
点评:本题考查函数的奇偶性与函数的单调性,以及它们的综合应用,函数值的大小比较,要利用单调性,统一在某个单调区间上比较大小.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
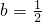 ,且k>0,问函数f(x)的图象是不是轴对称图形?如果是,求出函数f(x)图象的对称轴;如果不是,请说明理由.
,且k>0,问函数f(x)的图象是不是轴对称图形?如果是,求出函数f(x)图象的对称轴;如果不是,请说明理由. ,且k>0,问函数f(x)的图象是不是轴对称图形?如果是,求出函数f(x)图象的对称轴;如果不是,请说明理由.
,且k>0,问函数f(x)的图象是不是轴对称图形?如果是,求出函数f(x)图象的对称轴;如果不是,请说明理由.