题目内容
直线l1:x+3y-15=0与直线l2:3kx-y-6=0与两坐标轴正向围成的四边形有一个外接圆,则k=
1
1
.分析:由四点共圆可得此两条直线相互垂直,利用斜率之间的关系即可得出.
解答:解:如图所示, 设l1∩l2=B.
设l1∩l2=B.
∵l1、l2及两坐标轴正向围成的四边形有一个外接圆,又∠AOC=90°.
∴∠ABC=90°.
∴kl1•kl2=-1,得-
×(3k)=-1,解得k=1.
故答案为1.
 设l1∩l2=B.
设l1∩l2=B.∵l1、l2及两坐标轴正向围成的四边形有一个外接圆,又∠AOC=90°.
∴∠ABC=90°.
∴kl1•kl2=-1,得-
| 1 |
| 3 |
故答案为1.
点评:熟练掌握四点共圆的条件、相互垂直的直线斜率之间的关系是解题的关键.

练习册系列答案
相关题目
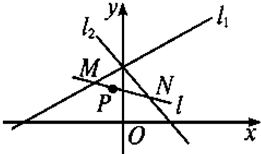 如图,已知两条直线l1:x-3y+12=0,l2:3x+y-4=0,过定点P(-1,2)作一条直线l,分别与l1,l2交于M、N两点,若P点恰好是MN的中点,求直线l的方程.
如图,已知两条直线l1:x-3y+12=0,l2:3x+y-4=0,过定点P(-1,2)作一条直线l,分别与l1,l2交于M、N两点,若P点恰好是MN的中点,求直线l的方程.